Примеры решения задач.

Рисунок 18

1. Построить три проекции геометрического тела и линию пересечения его поверхности с плоскостью S.

2. Найти натуральную величину фигуры полученной в пересечении.

3. Построить полную развертку усеченной части геометрического тела.

4. Из чертежной бумаги выполнить модель усеченной части геометрического тела.

Алгоритм решения

1. Строим три проекции призмы.

2. Находим линию пересечения секущей плоскости с поверхностью призмы. При пересечении призмы с плоскостью S (S₂) в данном случае получается 4-х угольник, вершинами которого являются точки пересечения секущей плоскости с ребрами и верхним основанием призмы, а именно, при пересечении плоскости S (S₂) с ребром А (А₂) получаем точку 1 (1₂), с ребром В (В₂) – точку 2 (2₂) и в пересечении с верхним основанием - точки 3 и 4 í(3₂) º (4₂)ý. Находим недостающие проекции точек, используя свойства поверхности и методы нахождения точек на них. Соединяем полученные точки между собой последовательно и с учетом видимости.

3. Определяем натуральную величину фигуры, полученной в пересечении плоскости S с призмой методом вращения. В качестве оси вращения выбираем фронтально проецирующую прямую i, проходящую через точку 1. Фронтальные проекции точек 1, 2, 3, 4 будут перемещаться по окружностям и займут положение, соответственно, ₂, ₂, ₂, и ₂ , а горизонтальные проекции – по прямым, перпендикулярным оси вращения i (i₁) и вертикальным линиям связи, в пересечении с которыми получим новое положение точек ₁, ₁, ₁, и ₁. Соединив последовательно горизонтальные проекции точек получим натуральную величину фигуры сечения.

4. Строим полную развертку усеченной части призмы. (Построение разверток геометрических тел описано выше). Для построения полной развертки усеченной части призмы необходимо найти на развертке точки 1, 2, 3 и 4, последовательно их соединить и пристроить нижнее основание, часть верхнего основания и натуральную величину фигуры сечения.

5. Склеиваем из чертежной бумаги модель усеченной части конуса с призматическим отверстием.

На рисунке 23 приведен пример выполнения задачи 1.

Задача 2 (Рисунок 18)

Построить три проекции конуса с вырезом.

Рисунок 18

Алгоритм решения

1. Строим три проекции конуса в тонких линиях (рисунок 19).

2. Определяем, каким количеством плоскостей образован вырез, и какая фигура получается в пересечении поверхности с этими плоскостями. В данном примере вырез образован 3-мя плоскостями: плоскость S (S₂) в пересечении с конусом дает параболу, плоскость Y (Y₂) – гиперболу, а плоскость Г (Г₂) – окружность.

Рисунок 19

3. Определяем точки пересечения секущих плоскостей с характерными (очерковыми) образующими конуса – 1(1₂), 2,3 (2₂ º 3₂), 8,9 (8₂ º 9₂), 10 (10₂); точки пересечения плоскостей между собой 4, 5, 6, 7 (4₂ º 5₂) и (6₂ º 7₂). Кроме этих точек определяем промежуточные точки для построения параболы и гиперболы.

4. Находим горизонтальные и профильные проекции названных точек методом секущих плоскостей.

5. Соединяем последовательно полученные точки с учетом видимости. Т.к. на горизонтальной проекции видны все точки, лежащие на боковой поверхности конуса, то соединяем линией видимого контура точки 1₁– 2₁– 4₁ и 1₁– 3₁– 5₁ (ветви параболы); 4₁– 6₁ и 5₁– 7₁ (ветви гиперболы); 6₁– 8₁– 10₁ и 7₁– 9₁– 10₁ (части окружности). Между точками 4₁– 5₁ и 6₁– 7₁ проводим линии невидимого контура, которые получаются за счет пересечения плоскостей S и Y и Y и Г.

На профильной проекции видимыми будут все линии пересечения:

1₃– 2₃– 4₃ и 1₃– 2₃– 4₃ (ветви параболы), 4₃– 6₃ и 5₃ – 7₃ (ветви гиперболы), линия 8₃– 10₃– 9₃, в которую проецируется окружность, а также линия пересечения плоскостей S и Y 4₃– 5₃.

6. На профильной плоскости проекции обводим очерк конуса: левую и правую очерковые образующие соответственно – от вершины до точек 3₃ и 2₃ и от точек 9₃ и 8₃ до линии основания.

Задача 3 (Рисунок 20а)

(Построить три проекции прямого кругового цилиндра и найти недостающие проекции заданных точек, лежащих на его поверхности)

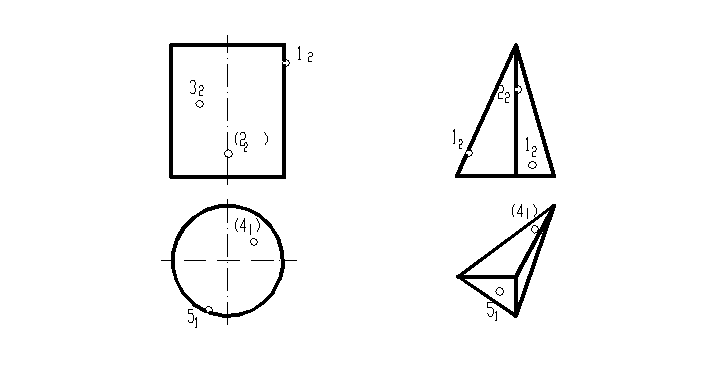
а) б)

Рисунок 20

Алгоритм решения

Строим три проекции цилиндра

Находим недостающие проекции заданных точек, используя свойства цилиндрической поверхности: все точки и линии, лежащие на боковой поверхности цилиндра, на горизонтальной проекции располагаются на дуге окружности основания. Т.к. точка 1(1₂) расположена на правой очерковой образующей цилиндра В (В₂), которая на П₁ проецируется в точку В₁ (прямая горизонтально проецирующая), то и горизонтальная проекция точки 1 (1₁) совпадает с проекцией этой образующей. Аналогичным образом находим горизонтальную проекцию точки 2, расположенной на дальней образующей цилиндра. Горизонтальную проекцию точки 3, расположенной на боковой поверхности цилиндра, находим на пересечении вертикальной линии связи из точки 3₂ и дуги окружности основания.

Рисунок 21

Профильные проекции точек 1(1₃) и 2(2₃) находим на пересечении горизонтальных линий связи, проведенных, соответственно, из точек 1₂ и 2₂ и образующих В(В₃) и D(D₃). Для построения профильной проекции точки 3(3₃) замеряем расстояние от базовой плоскости Ф₁ до точки 3₁ и откладываем его от Ф₃ по горизонтальной линии связи, проведенной из точки 3₂.

Т.к. на горизонтальной проекции видны только точки, лежащие на верхнем основании, то точка 4, заданная невидимой, принадлежит нижнему основанию, а точка 5, по заданию видимая, расположена на верхнем основании. На П₂ проекции этих точек находим на пересечении вертикальных линий связи, проведенных из заданных горизонтальных проекций точек 4₁ и 5₁ с линиями нижнего и верхнего оснований.

Профильные проекции точек 4(4₃) и 5(5₃) находим замеряя расстояния от базовой плоскости Ф₁ до точек 4₁ и 5₁ и откладывая их от Ф₃, соответственно, по линии нижнего и верхнего оснований.

Задача 4 (Рисунок 20б)

(Построить три проекции треугольной пирамиды и найти недостающие проекции заданных точек, лежащих на ее поверхности)

Алгоритм решения

Строим три проекции пирамиды, используя для построения профильной проекции базовую плоскость Ф, проведенную через точку А.

Рисунок 22

По заданным проекциям точек находим их недостающие проекции.

Находим горизонтальную и профильную проекции точки 1 (1₁ и 1₃) на пересечении горизонтальной и вертикальной линий связи, проведенных из точки 1₂ с проекциями ребра AS (A₁S₁ и A₃S₃).

Точка 2 задана на ребре SB. Горизонтальную проекцию точки 2(2₁) находим методом секущей плоскости: через заданную проекцию точки 2₂ проводим горизонтальную плоскость уровня Г(Г₂), которая в пересечении с поверхностью пирамиды дает треугольник подобный основанию. Строим горизонтальную проекцию этого треугольника через вспомогательные точки, расположенные на ребрах AS (A₂S₂) CS(C₂S₂). На пересечении вершины построенного треугольника и ребра SB найдем горизонтальную проекцию точки 2(2₁). Профильную проекцию точки 2(2₃) найдем на пересечении горизонтальной линии связи, проведенной из точки 2₂ и ребра SB (S₂B₂).

Недостающие проекции точек 5 (5₂) и 3 (3₁) находим методом образующей: через вершину S и заданные проекции точек проводим прямую линию (образующую) до пересечения со стороной основания, строим проекции этих образующих и на них находим искомые проекции точек.

Профильные проекции точек 5(5₃) и 3(3₃) находим замеряя расстояния от базовой плоскости Ф₁ до точек 5₁ и 3₁ и откладывая их от Ф₃ по горизонтальным линиям связи, проведенным из точек 5₂ и 3₂.

Т.к. точка 4(4₁) задана невидимой, значит она расположена на основании пирамиды и для ее нахождения на П₂ достаточно провести вертикальную линию связи до пересечения с линией основания, а на П₃ – замерить расстояние от базовой плоскости Ф(Ф₁) до горизонтальной проекции точки 4(4₁) и отложить его на П₃ по линии основания.

Контрольные вопросы

1. Что называется многогранником?

2. Что является сечением поверхности многогранника плоскостью?

3. Какие способы построения сечения многогранника плоскостью существуют? В чем заключаются эти способы?

4. Как формируется алгоритм построения точек пересечения прямой с поверхностью многогранника?

5. Что называется поверхностью вращения?

6. Укажите основные свойства поверхностей вращения.

7. Какие линии на поверхности вращения называются: параллелью, экватором, горлом, меридианом, главным меридианом?

8. Какие фигуры могут быть получены при рассечении плоскостью кругового цилиндра, конуса, сферы? В каких случаях эти поверхности рассекутся по графически простым линиям?

9. Назовите методы нахождения точек на поверхностях вращения.

10. Какие точки линии пересечения поверхности с плоскостью называются опорными, промежуточными?

11. Сформулируйте алгоритм нахождения точек пересечения прямой с поверхностью вращения.

12. Как строятся развертки многогранных поверхностей (призмы и пирамиды)?

13. Как строятся развертки поверхностей вращения (цилиндра, конуса, сферы)?

Рисунок 23 - Пример выполнения листа 1 задания 4

Рисунок 24 – Пример выполнения листа 2 задания 4

Задание 4 «Пересечение поверхностей»