ВИДЫ ПОТЕРЬ НАПОРА

Различают два вида потерь напора:

потери напора на преодоление гидравлических сопротивлений по длине , вызываемых трением жидкости о стенку трубы и слоев жидкости друг о друга;

местные потери напора , возникающие только в отдельных местах потока, где наблюдается его деформация (задвижка, поворот, резкое сужение или расширение трубы и т.п.).

Общую величину потерь напора для участка трубопровода, заключенного между двумя сечениями, определяют как сумму потерь напора по длине рассматриваемого участка и всех местных потерь напора

. (4.1)

Потери напора для плавноизменяющегося движения определяются из уравнения Бернулли (3.11)

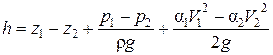. (4.2)

Из выражения (4.2) следует, что для определения общих потерь напора необходимо измерить разности геометрических, пьезометрических и скоростных напоров. При равномерном потоке в горизонтальной трубе потери напора определяются по формуле

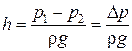, (4.3)

т.е. потери напора определяются как разность показаний пьезометров в крайних сечениях участка трубопровода.

4.2. МЕТОД ТЕОРИИ РАЗМЕРНОСТЕЙ И ЕГО ПРИЛОЖЕНИЕ К ВЫВОДУ
ОБЩИХ ФОРМУЛ ДЛЯ ОПРЕДЕЛЕНИЯ ПОТЕРЬ НАПОРА

Метод теории размерностей широко применяется во многих исследованиях. Начало общей теории этого метода было положено в 1911 г. русским ученым А. Федерманом, доказавшим фундаментальную теорему подобия, частным случаем которой является теорема о размерности, известная под названием " -теорема". Согласно этой теореме, всякое уравнение, выражающее некоторую физическую закономерность и потому не зависящее от выбора системы единиц измерения, связывающее между собой k физических величин, среди которых n величин обладают независимыми размерностями, может быть преобразовано в уравнение, связывающее k-n независимых безразмерных комплексов, составленных из упомянутых k физических величин.

При установившемся движении жидкости средняя скорость течения V и перепад давлений 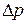зависят от физических свойств жидкости, размеров трубопровода, в котором происходит изучаемое движение жидкости, и шероховатости стенок трубы.

Физические свойства жидкостей определяются такими размерными характеристиками, как плотность и вязкость m размеры трубопровода - диаметром d и длиной l, а шероховатость стенок трубы оценивается средним значением линейных размеров выступов шероховатости .

Взаимосвязь между перечисленными параметрами можно выразить в виде уравнения

, (4.4)

где - потери давления на единицу длины трубы.

В выражении (4.4) выделим три основные величины V, d, с независимыми размерностями. Размерность любой из этих величин нельзя получить из комбинации размерностей двух других, в то же время через размерности V, d и можно выразить размерность любой другой величины, входящей в рассматриваемую зависимость. Обозначив любую из остальных величин через , найдем, что размерности этих величин являются зависимыми и определяются через размерности основных величин выражением

,

где x, y, z - показатели степени, при которых размерности обеих частей выражения одинаковы.

Отсюда ,

где - размерности длины, времени и массы.

Отношение дает некоторое отвлеченное число, представляющее собой безразмерный комплекс, получивший название -члена

.

Таким образом, на основании -теоремы выражение (4.4) можно привести к функциональной зависимости между безразмерными комплексами, составленными из рассматриваемых размерных величин

. (4.5)

Найдем эти безразмерные комплексы, для чего напишем условия равенства размерности числителя и знаменателя последовательно для каждого из них.

Для первого комплекса 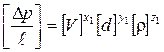или, выражая размерности величин через размерности длины, времени и массы,

.

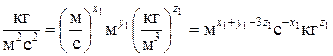Приравнивая показатели степени при одноименных размерностях, получаем три уравнения

из которых находим

Первый безразмерный комплекс примет вид

.

Из уравнения равенства размерности для второго комплекса

или получим систему уравнений:

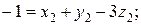
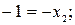
решение которых определяет

Второй безразмерный комплекс запишется в виде , что соответствует величине, обратной числу Рейнольдса .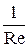

Из уравнения равенства размерности для третьего комплекса

или

получим уравнения из которых найдем

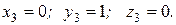
Третий безразмерный комплекс запишется в виде .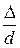

Общая функциональная зависимость примет вид

.

Умножая числитель и знаменатель левой части данной зависимости на g и учитывая, что есть выражение линейных потерь напора h_l, запишем

После умножения обеих частей выражения на 2 находим

. (4.6)

Обозначим безразмерную величину

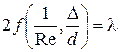, (4.7)

которую принято называть коэффициентом сопротивления трения по длине трубы или коэффициентом Дарси.

Подставив в зависимость (4.6), получим формулу для определения потерь напора по длине

. (4.8)

Из формулы (4.8) следует, что потери напора по длине возрастают с увеличением средней скорости потока и длины трубы и обратно пропорциональны диаметру трубы. Преждевременно делать вывод, что потери напора пропорциональны квадрату скорости, так как не раскрыта функция (4.7), определяющая величину , которая, как это будет показано в дальнейшем, для некоторых случаев движения жидкости сама зависит от V. Формула (4.8) была получена в XIX в. эмпирическим путем и называется формулой Дарси – Вейсбаха.

Приведенный метод можно использовать для определения вида формулы местных потерь напора. Учитывая, что местные потери зависят от типа местного сопротивления и практически не зависят от длины участка, функциональную зависимость можно представить в следующем виде:

. (4.9)

В нее вошла наряду с известными размерными величинами безразмерная , характеризующая соотношение геометрических размеров местных сопротивлений.

В соответствии с -теоремой запишем зависимость (4.9) в форме, содержащей безразмерные комплексы

. (4.10)

Показатели степени V, d и определим, как это было показано выше, сравнением размерностей при одноименных единицах измерения.

В результате найдем и первый безразмерный комплекс получит вид

.

Второй безразмерный комплекс уже был нами получен, он записывается в виде

.

Общая функциональная зависимость после известных преобразований будет иметь вид

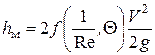. (4.11)

Численное значение функции обозначают z и называют коэффициентом местного сопротивления.

В окончательном виде формула для определения местных потерь напора запишется

. (4.12)

Формула (4.12) была получена в XIX в. эмпирическим путем и называется формулой Вейсбаха.