ВЛИЯНИЕ РЕЖИМА ДВИЖЕНИЯ ЖИДКОСТИ НА ПОТЕРИ НАПОРА

Различия в условиях движения жидкости при ламинарном и турбулентном режимах порождают соответствующие изменения потерь напора.

Построим график h = f(V), замеряя потери напора при движении воды в трубе с различной скоростью (рис. 4.2).

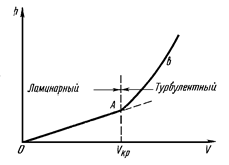
Рис. 4.2. График зависимости потерь напора от средней скорости

Потери напора при ламинарном режиме пропорциональны первой степени средней скорости потока

где 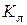- коэффициент пропорциональности при ламинарном режиме.

На графике (см. рис. 4.2) ламинарному движению жидкости соответствует отрезок 0A, имеющий вид прямой линии.

При турбулентном режиме потери напора пропорциональны средней скорости в степени

,

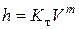где - коэффициент пропорциональности при турбулентном режиме; 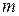- показатель степени, обычно равный 1,75 - 2.

Таким образом, ламинарный и турбулентный режимы движения жидкости характеризуются разными зависимостями для потерь напора.

4.5. РАСПРЕДЕЛЕНИЕ СКОРОСТЕЙ ПО СЕЧЕНИЮ ТРУБЫ
И ПОТЕРИ НАПОРА ПРИ ЛАМИНАРНОМ ДВИЖЕНИИ

Рассмотрим ламинарный поток с равномерным движением в прямой круглой трубе радиусом (рис. 4.3). Применим к нему основное уравнение равномерного движения и определим закон распределения скоростей по сечению трубы и величину коэффициента гидравлического трения.

Рис. 4.3. Распределение скоростей и касательных напряжений

при ламинарном движении

Согласно выражению (4.15), имеем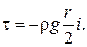

С другой стороны, касательные напряжения в жидкости определяются по формуле (1.10) как

.

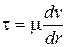Приравнивая правые части этих выражений, определяем

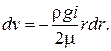
Интегрируя это уравнение, получаем .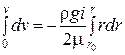

Получим общее выражение для скорости в любой точке живого сечения при ламинарном режиме

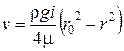. (4.22)

Как видно из уравнения (4.22), кривая распределения скоростей является параболой (см. рис. 4.3). Скорость максимальна в центре трубы 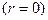и она определяется выражением

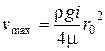. (4.23)

Тогда вместо формулы (4.22) можно записать

(4.24)

или (4.25)

Следовательно, отношение местной скорости в точке живого сечения трубы к максимальной скорости зависит только от относительного положения точки в сечении трубы .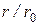

Иначе говоря, эпюры относительных скоростей во всех равномерных ламинарных потоках в круглых трубах подобны и могут быть представлены одной параболой, построенной по уравнению (4.25).

Вычислим значение средней скорости. Для этого определим расход через трубу как сумму элементарных расходов через кольца радиуса r шириной dr (рис. 4.4.):

Подставив сюда значение v из выражения (4.24), найдем

.

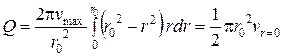Разделив расход на площадь живого сечения , получим

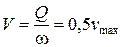. (4.26)

То есть средняя скорость ламинарного потока в круглой трубе равна половине максимальной скорости.

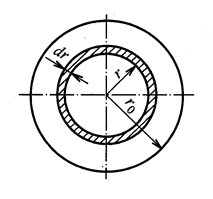
Рис. 4.4. К определению средней скорости в ламинарном потоке

Подставляя в выражение (4.26) значение максимальной скорости из формулы (4.23), получаем выражение для средней скорости

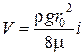. (4.27)

Откуда (4.28)

Потери напора по длине, согласно формуле (3.12), будут равны

.

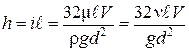Эта формула показывает, что потери напора на трение при ламинарном режиме пропорциональны первой степени средней скорости движения жидкости. Отсутствие в формулах (4.21) и (4.28) параметров, характеризующих состояние стенок, говорит о том, что потери напора в данном случае не зависят от шероховатости внутренней поверхности трубы, т.е. имеет место только трение жидкости о жидкость, а не жидкости о стенку.

Сопоставляя выражение (4.28) с общей зависимостью для потерь напора на трение (4.8), найдем формулу для определения коэффициента гидравлического трения

. (4.29)

Выражение (4.29) носит название формулы Пуазейля – Стокса.

4.6. КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ И РАСПРЕДЕЛЕНИЕ
СКОРОСТИ В ТУРБУЛЕНТНОМ ПОТОКЕ

Как уже отмечалось, для турбулентного режима характерно перемешивание жидкости, пульсация скоростей и давлений в процессе движения. Вследствие чрезвычайной сложности происходящих явлений механизм турбулентного потока изучен далеко не полностью. В основе современных представлений о турбулентности лежит теория переноса количества движения, развитая Прандтлем.

Рассмотрим поток жидкости, в котором элементарные частицы благодаря поперечной пульсационной скорости переносятся из одного слоя в другой. В силу неразрывности потока одновременно с перемещением частицы из первого слоя во второй другая частица перемещается из второго слоя в первый. Так как скорости перемещающихся частиц различны, то в каждом из слоев происходит изменение количества движения, приводящее к возникновению дополнительного напряжения на границе соприкосновения слоев

(4.30)

где 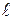- длина пути перемешивания, на котором элементарная частица жидкости, переходя из одного слоя в другой, приобретает скорость последнего; 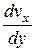- градиент скорости.

Величина должна быть добавлена к тому чисто вязкостному напряжению, которое действует между отдельными слоями турбулентного потока.

Общее касательное напряжение при турбулентном режиме будет равно

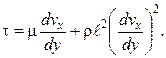(4.31)

При ламинарном режиме, ввиду отсутствия перемешивания жидкости при 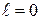, касательное напряжение 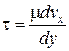пропорционально градиенту, а следовательно, и скорости потока, так как при постоянстве эпюры скоростей градиенты скорости прямо пропорциональны средней скорости потока.

При турбулентном движении с резко выраженным перемешиванием масс жидкости второй член в уравнении (4.31) значительно возрастает по сравнению с первым, так что вязкостной частью напряжений можно пренебречь (за исключением зоны в непосредственной близости к стенке).

Следовательно, при развитой турбулентности касательные напряжения пропорциональны квадрату средней скорости. В этих случаях, наиболее часто встречающихся в гидротехнической практике, говорят о квадратичной области сопротивления.

Наконец, уравнение (4.31) показывает, что в тех случаях, когда напряжение от сил вязкости соизмеримо с дополнительными напряжениями, общее касательное напряжение будет пропорционально средней скорости в степени, несколько меньше второй. В таких случаях говорят о переходной области сопротивления.

Полученные из анализа уравнения (4.31) выводы хорошо подтверждаются опытными данными.

Наличие перемешивания в турбулентном потоке и связанного с ним переноса количества движения из одного слоя жидкости в другой должно приводить к определенному выравниванию скоростей в различных точках живого сечения. На рис. 4.5 показана эпюра скоростей в круглой трубе при турбулентном режиме. Из него видно, что как и при ламинарном режиме скорости весьма быстро возрастают в прилегающем к стенке слое незначительной толщины, а затем, благодаря влиянию перемешивания, дальнейшее их возрастание до максимального значения по оси трубы происходит очень медленно.

В отличие от ламинарного потока, характеризующегося отношением 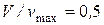, в турбулентном потоке это отношение меняется и составляет, например, для труб 0,75 при 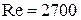; 0,9 при 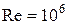; 0,96 при 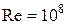и т.д., приближаясь к единице с увеличением числа Рейнольдса.

Рис. 4.5. Распределение скоростей при турбулентном движении

В пределе при 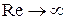будет совершенно равномерная эпюра скоростей по сечению потока, характерная для невязкой жидкости. Этого и следовало ожидать, так как движение невязкой жидкости можно характеризовать как движение при .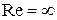

Распределение скоростей в турбулентном потоке, согласно формуле Прандтля, выражается зависимостью

(4.32)

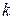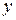где - универсальная постоянная Прандтля, равная по опытам Никурадзе 0,4; - радиус трубы; - расстояние рассматриваемой точки от стенки трубы; 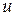- так называемая динамическая скорость, или скорость касательного напряжения.

Динамическую скорость определяют по формуле 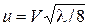, входящей в выражение (4.18).

Современные исследования подтверждают справедливость формулы (4.32), но при условии, что 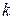- величина переменная.

Приблизительно распределение скоростей в поперечном сечении трубы при турбулентном режиме описывается уравнением

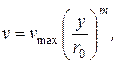(4.33)

где 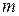- показатель степени, зависящий от шероховатости стенок трубы и числа 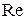, по А.Д. Альтшулю, 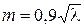, изменяется в пределах 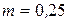для шероховатых труб до 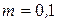для гладких труб.

4.7. ПОНЯТИЕ О ГИДРАВЛИЧЕСКИХ ГЛАДКИХ И ШЕРОХОВАТЫХ
ТРУБАХ

Предположим, что при турбулентном движении потока жидкости в трубе радиусом 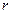выступы шероховатости внутренней поверхности имеют высоту . В пограничном слое жидкости, примыкающем непосредственно к стенке, которая ограничивает поперечное перемещение частиц, может наблюдаться параллельно-струйное ламинарное движение. Этот слой называют ламинарным слоем в отличие от турбулентного ядра в центральной части потока. Толщина ламинарного слоя изменяется в зависимости от скорости движения жидкости и измеряется обычно долями миллиметра. Она может быть определена по формуле

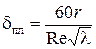. (4.34)

Если ламинарный слой, обволакивающий выступы шероховатости, полностью их перекрывает (рис.4.6, а), то потери напора не будут зависеть от степени шероховатости стенок трубы: в этом случае жидкость будет скользить по ламинарному слою, вызывая трение жидкости о жидкость. И хотя в целом режим движения турбулентный, но выступы шероховатости погружены в ламинарный слой, коэффициент будет зависеть, как при ламинарном режиме, только от числа 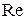. Условие существования гидравлически гладких труб можно записать в виде .

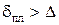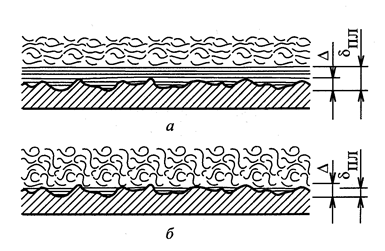
Рис. 4.6. Схемы течения жидкости в трубах:

а - гидравлически гладких; б - гидравлически шероховатых

С увеличением числа Re, согласно уравнению (4.34), ламинарный слой становится тоньше и выступы шероховатости (рис. 4.6, б) попадают в турбулентное ядро. Они становятся дополнительными очагами возмущения потока, позади выступов создаются вихри, на образование которых затрачивается механическая энергия движения жидкости. Условие существования гидравлически шероховатых труб запишется в виде d_пл < D.

Отсюда ясно, что понятия гидравлически гладкой и шероховатой поверхности - относительные: одна и та же труба при малых числах Re может быть гладкой, а при больших числах Re - шероховатой.

Следует отметить, что кроме двух рассмотренных случаев турбулентного движения жидкости встречается и некоторый промежуточный вариант как переходный между ними. Такое явление наблюдается, если высота выступов шероховатости имеет тот же порядок, что и толщина пограничного ламинарного слоя.

4.8. ЭКСПЕРИМЕНТАЛЬНОЕ ИЗУЧЕНИЕ КОЭФФИЦИЕНТА
ГИДРАВЛИЧЕСКОГО ТРЕНИЯ

В отличие от ламинарного движения, при котором формула для коэффициента гидравлического трения была получена теоретически, при турбулентном движении для нахождения расчетных формул приходится прибегать к помощи экспериментальных исследований.

Трудность решения этой проблемы обусловливается сложностью процессов, совершающихся в турбулентном потоке, определяющее влияние на который оказывает шероховатость стенок трубопроводов. Шероховатость, в свою очередь, зависит от материала трубы, характера механической обработки внутренней поверхности, наличия или отсутствия в трубе коррозии, отложения осадков и т.д.

Экспериментальные работы по исследованию коэффициента l выполнялись в трубах как с искусственной, так и с естественной шероховатостью. Искусственная шероховатость создавалась следующим образом: внутренние стенки труб сначала покрывались лаком, затем труба заполнялась песком определенной зернистости (со средним диаметром D), приклеивавшимся к стенкам однородным слоем. После этого бугристая поверхность вновь покрывалась лаком и высушивалась. Относительная шероховатость характеризовалась отношением D/d, а относительная гладкость R/D и d/D. Естественная шероховатость промышленных трубопроводов в настоящее время характеризуется некоторой величиной D, эквивалентной искусственной шероховатости, вызывающей в трубопроводе того же размера при одних и тех же числах Re и расходах одинаковые потери удельной энергии.

С помощью анализа размерностей было установлено, что коэффициент гидравлического трения l в формуле Дарси – Вейсбаха (4.8) может зависеть от двух безразмерных параметров, представляющих собой число Рейнольдса и относительную шероховатость.

Наиболее полные исследования по определению коэффициента l впервые были выполнены Никурадзе, который по результатам опытов построил график зависимости lgRe от lg(100l) для труб с различной сте-пенью шероховатости (рис. 4.7). Анализ графика Никурадзе позволяет выделить пять областей, каждая из которых характеризуется своими закономерностями.

Первая - область ламинарного режима (прямая 1), в пределах которой l = 64/Re при Re £ 2320.

Вторая - область перехода ламинарного режима к турбулентному. В небольшом интервале 3,3 < lgRe < 3,5 опытные точки располагаются достаточно кучно для всех значений шероховатости.

Третья - область турбулентного движения в гидравлически гладких трубах (прямая 3), с которой совпадают опытные точки до некоторых чисел Рейнольдса. В этой области коэффициент l изменяется только в зависимости от Re и не зависит от шероховатости трубы.

В области гладких труб при значениях чисел Рейнольдса до 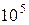для определения коэффициента l применяется формула Блазиуса:

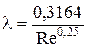. (4.35)

Рис.4.7. График зависимости l = f(Re, ) для труб с равномерной шероховатостью

Четвертая - область турбулентного движения, в которой значения коэффициента l в зависимости от шероховатости трубы располагаются вдоль индивидуальных линий между прямой 3 и линией АВ. Здесь l зависит как от шероховатости, так и от числа Рейнольдса. Эта область называется промежуточной.

Пятая - область турбулентного движения в гидравлически шерохова-тых трубах; она располагается правее линии АВ и представлена горизонтальными линиями, указывающими на то, что здесь коэффициент l зависит только от шероховатости.

Если l не зависит от Re, то из формулы (4.8) следует, что в пятой области потери напора пропорциональны квадрату скорости, поэтому область называется квадратичной.

Для определения l в квадратичной области сопротивлений можно использовать формулу Шифринсона, которая применима при Re > 500:

. (4.36)

А.Д. Альтшуль предложил для определения l универсальную формулу, применяемую во всех областях турбулентного режима,

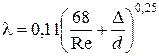. (4.37)

Справедливость этого выражения подтверждается тем, что при величиной 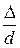можно пренебречь и формула (4.37) практически совпадает с формулой Блазиуса, а при Re 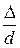> 500 - с формулой Шифринсона.

Для расчета водопроводных труб, бывших в эксплуатации, может быть рекомендована формула Ф.А. Шевелева, в которой [d] = М:

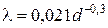. (4.38)

Итак, общая формула 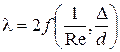отражает сложную закономер-ность, в которой в зависимости от величины Re влияние шероховатости на l либо не сказывается вовсе, либо играет настолько решающую роль, что влияние Re пропадает.