
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
МЕСТНЫЕ ПОТЕРИ НАПОРА
Местные потери напора при турбулентном режиме движения определяются по формуле (4.12). В принципе потери напора могут быть вычислены через скоростной напор как перед местным сопротивлением, так и за ним. Поэтому коэффициент местного сопротивления может быть отнесен к любому из этих скоростных напоров, но будет иметь разное значение - обратно пропорциональное скоростным напорам.
В некоторых случаях местные потери напора определяют по эквивалентной длине, понимая под последней такую длину прямого участка трубопровода, на которой линейные потери напора равны местным. Величину эквивалентной длины  найдем, приравнивая значения линейных и местных потерь напора, определяемых по формулам (4.8) и (4.12):
найдем, приравнивая значения линейных и местных потерь напора, определяемых по формулам (4.8) и (4.12):
 ,
,
откуда  . (4.39)
. (4.39)
В водопроводных трубах потери напора на местные сопротивления обычно невелики, составляют 5-20 % от потерь напора на трение по длине.
Рассмотрим наиболее типичные местные сопротивления.
Внезапное расширение трубопровода. Теорема Борда. Теоретическое определение местных потерь напора ввиду большой сложности происходящих явлений может быть выполнено только для немногих случаев, в частности для случая внезапного расширения трубопровода (рис. 4.8).

Рис. 4.8. Внезапное расширение трубопровода
Как показывают наблюдения, поток не обтекает контур внезапного расширения трубы, а образует более плавные линии токов. В кольцевом пространстве между струей и стенками трубы создается водоворотная зона, на протяжении которой имеет место неравномерное движение, местами резко изменяющееся.
Используя теорему об изменении количества движения для отсека жидкости ABCD, получаем формулу
 , (4.40)
, (4.40)
где разность (V1 - V2) называют потерянной скоростью.
Формула (4.40) называется формулой Борда. Согласно этой формуле, потери напора при резком расширении потока равны скоростному напору, отнесенному к потерянной скорости.
Учитывая, что 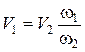 и
и  ,
,
можем записать  или
или  . (4.41)
. (4.41)
Обозначая  и
и  , (4.42)
, (4.42)
получим  или
или  . (4.43)
. (4.43)
Диффузор (рис. 4.9) характеризуется двумя параметрами: углом конусности Q и степенью расширения  . При протекании жидкости через диффузор основное влияние на конфигурацию потока оказывает угол конусности. Наиболее благоприятные условия создаются при плавном расширении потока (Q < 8¸10), когда на всем протяжении диффузора жидкость течет в одном направлении, не отрываясь от стенок. Однако с увеличением угла раскрытия диффузора (Q > 8¸10) в диффузоре появляются обратные течения, причем с увеличением угла Q точка отрыва струи от стенок перемещается вверх по течению.
. При протекании жидкости через диффузор основное влияние на конфигурацию потока оказывает угол конусности. Наиболее благоприятные условия создаются при плавном расширении потока (Q < 8¸10), когда на всем протяжении диффузора жидкость течет в одном направлении, не отрываясь от стенок. Однако с увеличением угла раскрытия диффузора (Q > 8¸10) в диффузоре появляются обратные течения, причем с увеличением угла Q точка отрыва струи от стенок перемещается вверх по течению.

Рис. 4.9. Диффузор
Потери напора в диффузоре выражают в долях потерь напора hв.р, вычисленных по формуле (4.40).
 , (4.44)
, (4.44)
где k - поправочный коэффициент, значения которого приведены в табл. 4.1.
Таблица 4.1
| Q, град | |||||||||||
| k | 0,12 | 0,13 | 0,15 | 0,17 | 0,26 | 0,41 | 0,71 | 0,90 | 1,03 | 1,12 | 1,13 |
Минимальные потери напора в диффузорах наблюдаются с углом расширения до 8°, а максимальные - при 70° и превосходят потери, соответствующие внезапному расширению. Из последнего следует, что переходы в виде диффузора с углом Q > 50° следует заменять внезапным расширением, как дающим меньшие потери напора.
Конфузор (рис. 4.10). Потери напора в конфузоре очень малы и становятся заметны при Q > 50°. При плавном сопряжении конической части с цилиндрической они практически равны нулю.

Рис. 4.10. Конфузор
Потери напора в конфузорах определяют по формуле
 , (4.45)
, (4.45)
где  - степень сужения конфузора.
- степень сужения конфузора.
Колена и закругления. Экспериментальные исследования показывают, что при повороте трубопровода на угол Q < 15° гидравлическим сопро-тивлением можно пренебречь. Коэффициент сопротивления для колена (рис. 4.11) при Q = 15¸90° можно определить по формуле Н.З. Френкеля
 . (4.46)
. (4.46)

Рис. 4.11. Колено
Значения для zк труб d < 50 мм приведены в табл. 4.2. С увеличением диаметра труб значение zк уменьшается.
Таблица 4.2
| Q, град | |||||||
| zк | 0,20 | 0,30 | 0,40 | 0,55 | 0,70 | 0,90 | 1,10 |
При плавном повороте трубы (рис. 4.12) вихреобразования уменьшаются и потери напора будут значительно меньше. Для определения коэффициента сопротивления закругления используют формулу Вейсбаха
 . (4.47)
. (4.47)

Рис. 4.12. Закругление
Значения zзак для разных соотношений r/R при Q = 90° приведены в табл. 4.3
Таблица 4.3
| r/R | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 |
| zзак | 0,13 | 0,14 | 0,16 | 0,21 | 0,29 | 0,44 | 0,66 | 0,98 | 1,41 | 1,98 |
Данными табл. 4.3 можно пользоваться и для других углов закругления Q ¹ 90°, умножая значение zзак на отношение Q / 90.
Вход в трубу из резервуара. Для коэффициента сопротивления следует принимать следующие значения: при острых кромках zвх = 0,5; закругленных - zвх = 0,2; весьма плавном входе - zвх = 0,05. В случае выхода из трубы в сосуд больших размеров zвых =1.
Следует отметить, что приведенные выше формулы относятся к турбулентному течению. При движении жидкости с малыми числами Re коэффициенты местных сопротивлений могут быть определены по формуле А.Д. Альтшуля:
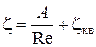 , (4.48)
, (4.48)
где zкв - значение коэффициента местного сопротивления в квадратичной области: Re - число Рейнольдса, отнесенное к нестесненному сечению трубопровода.
Значения А и zкв для некоторых местных сопротивлений приведены в табл. 4.4.
Таблица 4.4
| Устройство | А | zкв |
| Пробковый кран | 0,4 | |
| Вентиль: | ||
| обыкновенный | ||
| угловой | 0,8 | |
| шаровой клапан | ||
| Угольник | ||
| 90° | 1,4 | |
| 135° | 0,4 | |
| Колено 90° | 0,2 | |
| Выход из трубы в бак | ||
| Выход из бака в трубу | 0,5 | |
| Тройник | 0,3 | |
| Задвижка | ||
| Полностью открытая | 0,15 | |
| n = 0,75 | 0,2 | |
| n = 0,5 | ||
| n = 0,25 | ||
| Диафрагма | ||
| n = 0,64 | ||
| n = 0,4 | ||
| n = 0,16 | ||
| n = 0,05 |
В некоторых случаях потери напора на местные сопротивления (в пожарных гидрантах, колонках, водомерах и др.) определяют по формуле
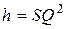 ,
,
аналогичной формуле (4.12), в которой средняя скорость V выражена через расход Q, а постоянная величина  - через сопротивление S.
- через сопротивление S.
4.10. ГИДРАВЛИЧЕСКИЙ РАСЧЕТ ТРУБОПРОВОДОВ.
Дата добавления: 2014-11-13; просмотров: 541; Мы поможем в написании вашей работы!; Нарушение авторских прав |