ПОТЕРИ НАПОРА, СРЕДНЯЯ СКОРОСТЬ И РАСХОД ПРИ РАВНОМЕРНОМ ДВИЖЕНИИ ЖИДКОСТИ

Установим зависимость между силами сопротивления и потерями напора при равномерном движении реальной жидкости. Для этого в трубе радиусом и площадью живого сечения выделим отсек жидкости длиной 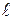, радиусом r и площадью сечения (рис. 4.1).

Координаты центров тяжести сечений относительно горизонтальной плоскости сравнения обозначим через и 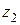, давления в них и .

Напряжение силы трения, возникающее между боковой поверхностью выделенного отсека и окружающей жидкостью, обозначим через .

На выделенный отсек действуют следующие силы:

сила тяжести , приложенная в его центре тяжести;

силы гидродинамического давления и , нормальные к сечениям I-I и II-II и направленные навстречу друг другу;

сила трения , возникающая на поверхности соприкосновения отсека с окружающей жидкостью, направленная в сторону, противоположную движению.

Рис. 4.1. К выводу уравнения равномерного движения

Составим уравнение равновесия перечисленных сил относительно оси потока:

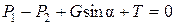. (4.13)

Подставляя в уравнение (4.13) выражение сил и принимая во внимание, что

,

будем иметь .

После деления всех членов на получим

.

Сравнивая это выражение с уравнением Бернулли (3.11) для случая равномерного движения и выражая через w/c гидравлический радиус потока R, получим основное уравнение равномерного движения жидкости

. (4.14)

Полученное выражение представим в несколько ином виде, выразив через гидравлический уклон

и . (4.15)

Так как радиус r выбран произвольно, то уравнение (4.15) может быть распространено на весь поток жидкости

, (4.16)

где - касательное напряжение на поверхности соприкосновения потока со стенками.

Из сравнения уравнений (4.15) и (4.16) получим

или .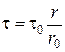

После замены 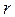на , где 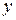- расстояние от стенки до поверхности отсека, получим для касательного напряжения в любом месте трубы следующую зависимость

. (4.17)

Таким образом, при равномерном движении касательное напряжение по сечению трубы изменяется по линейному закону. Оно равно нулю на оси трубы и достигает максимального значения у стенки .

Формулу для средней скорости получим из уравнения (4.8), выразив диаметр через гидравлический радиус,

. (4.18)

После замены 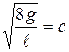и получим так называемую формулу Шези

, (4.19)

в которой величину с называют коэффициентом Шези.

Используя принятые обозначения, получим расчетные зависимости для расхода и потерь напора при равномерном движении:

; (4.20)

(4.21)

Для расчета потерь напора по длине (4.8) или (4.21) необходимо знать величину коэффициента сопротивления трения или коэффициента Шези с.