РАСЧЕТНЫЕ ФОРМУЛЫ

При гидравлическом расчете трубопроводов в зависимости от соотношения в них местных и линейных потерь напора различают короткие и длинные трубопроводы. К первым относят трубопроводы, в которых величина местных потерь напора превышает 10 % от потерь напора по длине. Короткими трубопроводами являются всасывающие линии насосных станций, сифоны, самотечные линии водоприемников, внутренние хозяйственно-питьевые водопроводы и т.п. При их расчетах обязательно указывают потери напора в местных сопротивлениях.

Ко вторым относят трубопроводы, имеющие значительную протяженность, в которых величина местных потерь напора не выше 10 % от потерь напора по длине. К длинным трубопроводам относят наружные водопроводные сети и водоводы, нефтепроводы и т.п.

В зависимости от схемы работы трубопроводы подразделяют на простые, одинаковые по диаметру, не имеющие ответвлений (рис. 4.13, а), и сложные, которые, в свою очередь, могут быть последовательно соединенными (рис. 4.13, б), параллельно соединенными (рис. 4.13, в) и разветвленными (рис. 4.13, г).

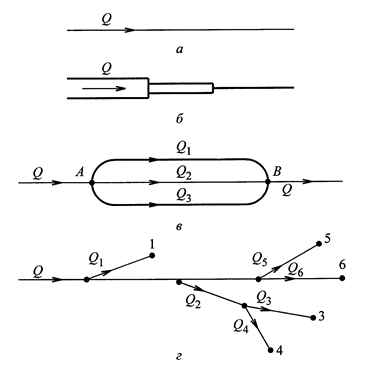
Рис. 4.13. Виды трубопроводов:

а - простой; б - последовательно соединенный;

в - параллельно соединенный; г - разветвленный

Гидравлический расчет трубопроводов сводится к решению трех основных задач: определению потерь напора, расхода воды, диаметра трубопровода при других заданных параметрах.

Для определения потерь напора пользуются формулой Дарси – Вейсбаха (4.8), которую можно привести к более простому виду.

Для этого определим среднюю скорость движения жидкости в трубе из условия неразрывности потока

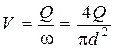
и подставим ее в уравнение Дарси – Вейсбаха

.

Обозначая отношение через А, получаем

. (4.49)

Величину А в формуле (4.49) называют удельным сопротивлением, она характеризует потери напора, приходящиеся на единицу длины трубы при единичном расходе, и имеет размерность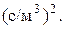

Произведение обозначают S и называют гидравлическим сопро-тивлением трубопровода.

Тогда 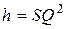. (4.50)

Из формулы (4.50) найдем выражения для расхода

, (4.51)

где - проводимость трубопровода.

При гидравлическом расчете напорных трубопроводов наряду с уравнением Дарси – Вейсбаха часто применяют уравнение для определения расхода жидкости (4.20), полученное из формулы Шези (4.19)

.

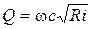Обозначая произведение 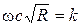, получаем

, (4.52)

где k - расходная характеристика, представляет собой расход жидкости в трубе заданного диаметра при гидравлическом уклоне, равном единице. Так как гидравлический уклон i - величина безразмерная, то из формулы (4.52) видно, что расходная характеристика k имеет размерность расхода жидкости.

Подставив в выражение (4.52) значение 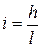и решив его относитель-но h, получим формулу для вычисления потерь напора:

. (4.53)

Сопоставляя (4.49) и (4.53), находим

. (4.54)

Таким образом, зная величины А и k, по формулам (4.49-4.51) и (4.53) можно провести гидравлический расчет трубопровода.

Учитывая, что в справочной литературе значения А и k даны для квадратичной области, при определении потерь напора в других областях работы трубопроводов в расчетные формулы необходимо внести поправку. Исследованиями Ф.А. Шевелева установлено, что квадратичная область в водопроводных трубах наступит при скорости движения жидкости V ³ 1,2 м/с. Поэтому при V < 1,2 м/с формулы (4.49) и (4.53) могут быть записаны в следующем виде:

, (4.55)

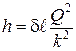, (4.56)

где d - поправочный коэффициент, величина которого зависит от скорости.

Последовательное соединение трубопроводов. При последовательном соединении труб (см. рис. 4.13, б) расход жидкости на всем пути остается постоянным, а общие потери напора во всей системе получают путем сложения потерь напора на отдельных участках

или с учетом формулы (4.50)

.

Выражение, стоящее в скобках, представляет собой сопротивление всей системы последовательно соединенных труб, т.е.

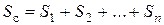. (4.57)

Тогда формула для потерь напора примет вид

. (4.58)

Следовательно, систему последовательно соединенных трубопроводов можно рассматривать как один простой трубопровод, сопротивление которого равно сумме сопротивлений составляющих его участков.

Параллельное соединение трубопроводов. При параллельном соединении (см. рис. 4.13, в) расход жидкости распределяется по ответвлениям, а потом снова сливается в точке схода и становится равным первоначальному. К узлам А и В мысленно подключим пьезометры, разность показаний которых будет равна потере напора в системе труб на пути от узла А до узла В

.

Очевидно, что потери напора на любом из параллельных участков также равны разности показаний пьезометров

.

Так как , то последнее выражение можно записать

.

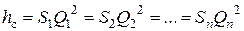Определим расходы на участках из этого соотношения

и найдем величину общего расхода жидкости

.

Отсюда 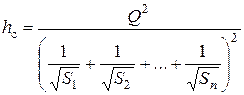(4.59)

или , (4.60)

где . (4.61)

Для частного случая, когда параллельные участки совершенно одинаковы, формула для определения сопротивления системы примет вид

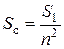, (4.62)

где S₁ - сопротивление одного из параллельных участков, n - число параллельных участков.

Трубопроводы с непрерывным расходом. Все установленные выше расчетные формулы относятся к случаям, когда по всему участку трубопровода между двумя точками проходит некоторый постоянный расход. Однако водоотбор может производиться и по длине трубопровода. Примером могут служить перфорированные трубопроводы, используемые в практике пожаротушения как системы орошения.

Основным вопросом расчета перфорированных трубопроводов является определение величины потерь напора. Рассмотрим случай, когда вода выходит из трубы равномерно по ее длине (рис. 4.14). На чертеже показана труба АВ длиной l и диаметром d. Эпюра I изображает расход воды из трубы. Расход, отдаваемый трубой с единицы длины, обозначим q, тогда величина всего отдаваемого расхода Q₀ будет равна ql. Очевидно, при равномерной отдаче воды на сторону расход Q в трубе уменьшается по линейному закону. Имея это в виду, эпюру расходов воды в различных живых сечениях потока можно представить трапецией II: правая крайняя ордината этой эпюры выражает так называемый транзитный расход Q_T, левая - расход в начальном сечении трубы Q (в точке А), который равен

.

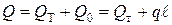Если обозначить расход Q_х в некотором живом сечении трубы х-х, то при изменениях х от 0 до l расход Q_х будет изменяться (по линейному закону) от величины (Q_T + ql) до величины Q_т, причем пьезометрический напор по мере уменьшения расхода будет также уменьшаться вдоль трубы. Пьезометрическая линия р-р будет кривой, причем выпуклость направлена вниз.

Qx

Рис. 4.14. Истечение жидкости из перфорированного трубопровода

Определим величину потерь напора для трубы АВ.

Для произвольного сечения трубы х-х имеем

.

На элементарном пути dx потеря напора равна

,

где А - удельное сопротивление трубопровода.

Подставляя вместо Q_x его значение (Q - qx), получаем

.

Интегрируя от х = 0 до х = l (т.е. для участка трубы от А до В), найдем

.

Так как ql = Q₀, то . (4.63)

Когда на участке сбрасывается весь расход (Q = 0), величина потери напора будет равна

. (4.64)

Из формулы (4.64) видно, что в случае непрерывного расхода по длине трубопровода потери напора в три раза меньше, чем при отсутствии отбора.