ОТВЕРСТИЯ В ТОНКОЙ СТЕНКЕ

Незатопленное отверстие (см. рис. 5.1). При истечении жидкости из отверстия задача сводится к определению скорости истечения и расхода жидкости. Составим уравнение Бернулли для сечения I-I и II-II относительно горизонтальной плоскости сравнения 0-0, проходящей через центр тяжести сжатого сечения струи:

,

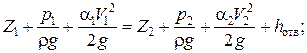
где р₁ - давление на свободной поверхности в сосуде; р₂ - давление в сечении II-II; z_отв - коэффициент сопротивления отверстия.

Величину 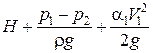обозначим Н₀ и назовем напором истечения.

Если сосуд имеет значительно большие размеры, чем отверстие, то скорость частиц V при истечении жидкости очень мала и членом 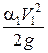можно пренебречь. В этом случае можно принять

.

Тогда из уравнения Бернулли получим: .

Отсюда скорость в сжатом сечении будет

или , (5.2)

где j - коэффициент скорости . (5.3)

Скорости в сжатом сечении струи практически одинаковы, поэтому можно принять α₂ = 1. Тогда

. (5.4)

Для воды, вытекающей из малого отверстия в тонкой стенке при , коэффициент скорости составляет 0,97.

Так как скорость определена в сжатом сечении с площадью w_c = εw, то расход жидкости из отверстия будет

или, подставляя значение скорости (5.2), получаем:

. (5.5)

Произведение коэффициентов скорости и сжатия называется коэффициентом расхода отверстия и обозначается μ₀:

. (5.6)

Опытным путем установлено, что коэффициент расхода для малых отверстий в тонкой стенке при совершенном сжатии равняется 0,62.

На практике чаще всего р₁ = р₂ = р_α, поэтому если пренебречь значением 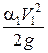по сравнению с Н₀, то напор истечения Н будет равняться просто глубине погружения центра тяжести отверстия Н. Поэтому формула для определения расхода жидкости примет вид:

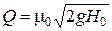. (5.7)

Затопленное отверстие (рис.5.3). Если пространство, куда вытекает жидкость, заполнено жидкостью, то имеет место истечение под уровень через затопленное отверстие. Расход может быть определен по уравнению Бернулли. Выберем два сечения на свободной поверхности в сосудах I-I и II-II, плоскость сравнения 0-0 проведем через центр тяжести отверстия в тонкой стенке.

Тогда имеем: .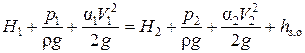

Пренебрегая скоростью и учитывая, что давление на поверхности жидкости с обеих сторон равно атмосферному, получаем:

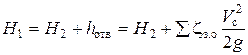
откуда ,

где DН - разность уровней воды; V_c - скорость протекания жидкости через сжатое сечение струи C-C; z_з.о - сумма коэффициентов сопротивления при протекание жидкости через затопленное отверстие, слагающаяся из коэффициента сопротивления на вход в тонкой стенке z_т.с и на внезапное расширение струи от сжатого сечения до сечения в резервуаре z_вр, равное единице.

Рис.5.3 Истечение жидкости через затопленное отверстие

Подставив значения коэффициентов сопротивлений в основное уравнение, найдем:

,

откуда скорость истечения равна .

Проведя преобразования и введя обозначение коэффициента истечения, получим формулу для расхода через затопленное отверстие

или . (5.8)

Исследования показали, что коэффициент расхода m_з.о для затопленного отверстия почти не отличается от m_о для незатопленного отверстия.