Опорожнение резервуаров

Для определения времени опорожнения резервуара емкостью с постоянным поперечным сечением по высоте (рис. 5.12) воспользуемся уравнением неразрывности, согласно которому объем жидкости, вытекшей из резервуара за время , равный , равен объему , освободившемуся в резервуаре при опускании уровня на :

. (5.17)

Рис. 5.12. Опорожнение резервуара постоянного
по высоте сечения

В общем случае расход жидкости через выходное сечение трубы при напоре равен

.

Подставив значение в уравнение (5.17), получим

,

откуда . (5.18)

Интегрируя, находим время , в течение которого уровень жидкости в резервуаре снизится от до :

. (5.19)

Для определения времени опорожнения резервуара необходимо учесть, что . Если же сливное отверстие находится на уровне дна резервуара, то , , и тогда

. (5.20)

Умножая числитель и знаменатель дроби на , получаем:

. (5.21)

Время истечения объема жидкости при постоянном напоре равно

. (5.22)

Сравнивая формулы (5.21) и (5.22), видим, что 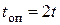, т.е. время опорожнение резервуара емкостью при начальном расходе в два раза больше времени истечения такого же количества жидкости при постоянном напоре и расходе .

Рассмотрим теперь случай опорожнения цилиндрического резервуара с горизонтальной осью. В этом случае является величиной переменной и зависит от Н. Прежде чем приступить к интегрированию дифференциального уравнения, вид которого не отличается от уравнения (5.18), необходимо выразить переменную в виде функции от . Пусть в некоторый момент уровень жидкости в резервуаре находится на высоте над отверстием (рис. 5.13). Площадь свободной поверхности жидкости представляет собой четырехугольник постоянной длины 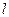и переменной ширины , которая вначале увеличивается до , а при дальнейшем понижении уровня ниже оси снова уменьшается до нуля.

Рис. 5.13. Схема опорожнения резервуара
переменного по высоте сечения

Как видно из рис. 5.13,

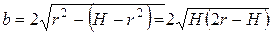
и, таким образом, .

Имея W = f(H), подставим его значение в уравнение (5.18)

,

где m₀ - коэффициент расхода при истечении жидкости через отверстие.

Проинтегрируем последнее выражение в пределах от до . Имея в виду, что , получим:

или, подставляя прeделы, 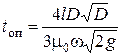, (5.23)

где - диаметр резервуара.

Использование постоянных коэффициентов сопротивлений позволяет получить лишь приближенное значение времени опорожнения, так как коэффициенты сопротивлений могут изменяться с изменением расхода. Однако в подавляющем большинстве случаев можно принимать, что происходит турбулентное истечение в квадратичной области гидравлических сопротивлений, в которой величина коэффициентов сопротивления остается постоянной.

Глава 6. ГИДРАВЛИЧЕСКИЕ СТРУИ