ТРАЕКТОРИЯ СПЛОШНОЙ СТРУИ

Рассмотрим случай, когда сплошная струя вылетает из насадка диаметром d с начальной скоростью V₀ и движется в воздушном пространстве подобно твердому телу, брошенному под углом Q к горизонту (рис. 6.4).

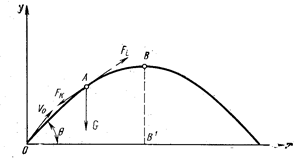
Рис. 6.4. Теоретическая траектория сплошной струи

Уравнения траектории струи, на которую действуют силы инерции 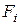, тяжести G и сопротивления воздуха 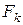, в параметрической форме могут быть представлены в виде:

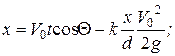(6.1)

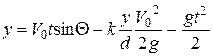, (6.2)

где x, y - координаты частицы струи в точке траектории; t - время; k - коэффициент сопротивления струи трению в воздухе.

Из уравнения (6.1) определим время:

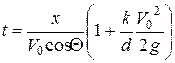
и, подставив в уравнение (6.2), получим:

. (6.3)

Заменяя в формуле (6.3) 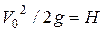, где H - напор у насадка, получаем уравнение траектории в общем виде:

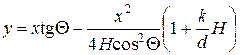. (6.4)

Найденное уравнение представляет собой непрерывную функцию f(x), имеющую максимум, следовательно, производная f(x) при этом значении обращается в нуль, т.е.

,

отсюда критическое значение: 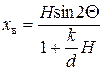. (6.5)

Подставляя выражение 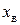в уравнение (6.4), получим максимальное значение функции:

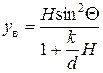. (6.6)

Из выражения (6.6) получим формулу для определения высоты вертикально направленной струи, принимая Q = 90^о,

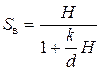. (6.7)

Теоретическую дальность полета струи 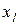определим из уравнения (6.4) при y = 0:

. (6.8)

Из выражения (6.8) видно, что максимальная теоретическая дальность полета струи будет при угле Q = 45^о

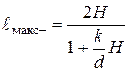. (6.9)

Из формул (6.6) и (6.9) видно, что теоретическая траектория по своей форме представляет собой параболу с вершиной в точке B ( 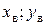), причем ось является осью симметрии параболы.

В действительности расчет по формуле (6.9) дает хорошее совпадение с данными, полученными опытным путем лишь при напорах истечения H = 3,5 - 7 м. При напоре 10 м наибольшая дальность полета достигается при 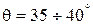, а при напоре 35 м – при . Причем наибольшее отклонение от теоретической траектории наблюдается в раздробленной части струи.

Несовпадение теоретических и практических данных объясняется сложной структурой струи, недостаточным знанием законов сопротивления, возникающего при движении струи в воздухе. Поэтому для расчета траекторий используются эмпирические данные.