
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ЭМПИРИЧЕСКИЕ ФОРМУЛЫ ДЛЯ РАСЧЕТА СПЛОШНОЙ СТРУИ
Вертикальная струя. Для расчета вертикальной струи обычно пользуются эмпирическими формулами Люгера и Фримана, полученными в конце XIX в. при изучении фонтанных и пожарных струй.
Рассмотрим струю жидкости, которая вылетает вертикально вверх из насадка с напором  и поднимается на высоту
и поднимается на высоту 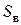 (рис. 6.5). Потерю высоты, вызванную сопротивлением воздуха, обозначим через
(рис. 6.5). Потерю высоты, вызванную сопротивлением воздуха, обозначим через  , а величину компактной части струи
, а величину компактной части струи 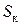 .
.
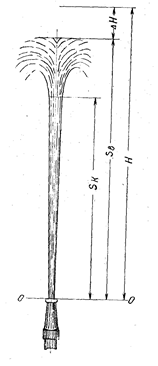 |
Рис. 6.5. Вертикальная струя
Высота вертикальной сплошной струи определится по формуле, предложенной Люгером, которая аналогична теоретической формуле (6.7):
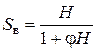 . (6.10)
. (6.10)
Коэффициент j может быть определен по эмпирической формуле
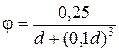 , (6.11)
, (6.11)
где d - диаметр выходного сечения насадка, мм.
Значение коэффициента j для различных диаметров насадков приведены в табл. 6.1.
Таблица 6.1
| d, мм | j | d, мм | j |
| 0,0228 | 0,0039 | ||
| 0,0165 | 0,0028 | ||
| 0,0124 | 0,0018 | ||
| 0,0097 | 0,0014 | ||
| 0,0077 | 0,00074 | ||
| 0,0061 | 0,00049 | ||
| 0,0050 | 0,00032 |
Фриман для расчета высоты вертикальных струй при напорах от 7 до
70 м предложил формулу
 . (6.12)
. (6.12)
Для практических расчетов формулы Люгера и Фримана можно считать равноценными.
Анализируя формулы (6.10) и (6.12), можно установить, что увеличение длины вертикальной струи связано с увеличением диаметра насадка и напора. Однако высота струи для каждого отдельного насадка не растет неограниченно, а достигает своей максимальной величины, после чего высота ее не изменяется, как бы сильно не увеличивался напор.
Из формулы Люгера найдем, что предельная величина Sв, которая получится при неограниченном увеличении H, будет равна:
 .
.
Так как величина j зависит только от диаметра (6.11), то отсюда следует, что при больших напорах увеличение высоты струи возможно только при увеличении диаметра насадка. Применение в пожарном деле лафетных стволов с насадками большого диаметра объясняется не только необходимостью большей подачи воды, но и возможностью подачи воды при обычных напорах на большое расстояние.
Исследуем теперь формулу Фримана. Приравнивая первую производную к нулю, получаем то значение H, при котором наблюдается максимальная высота струи:

Величины напоров, с достижением которых для определенного диаметра насадков струя не увеличивается, приведены в табл. 6.2.
Таблица 6.2
| d, мм | H, м | d, мм | H, м | d, мм | H, м |
Решая уравнение (6.10) относительно H, получаем формулу для определения напора в зависимости от требуемой высоты струи:
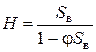 . (6.13)
. (6.13)
Величину компактной части струи определяют как часть всей вертикальной струи:
 . (6.14)
. (6.14)
Значение коэффициента a можно вычислить по эмпирической формуле Лобачева:
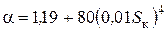 . (6.15)
. (6.15)
Величины коэффициентов α приведены в табл. 6.3.
Таблица 6.3
| Sк, м | ||||||||||||
| a | 1,19 | 1,20 | 1,21 | 1,22 | 1,24 | 1,27 | 1,32 | 1,38 | 1,45 | 1,55 | 1,67 | 1,84 |
| Sв, м | 9,5 | 14,5 | 17,2 | 23,0 | 26,5 | 30,5 | 47,0 |
Наклонная струя. Если при одном и том же напоре у насадка постепенно изменять угол наклона ствола, то конец компактной части струи будет описывать траекторию abc, которая называется огибающей кривой компактной струи, а наиболее удаленные капли струи - траекторию 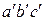 , называемую огибающей кривой раздробленной струи (рис. 6.6). Расстояния по прямой от насадка до граничных кривых соответственно называются радиусом действия компактной струи
, называемую огибающей кривой раздробленной струи (рис. 6.6). Расстояния по прямой от насадка до граничных кривых соответственно называются радиусом действия компактной струи  и радиусом действия раздробленной струи
и радиусом действия раздробленной струи 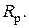

Рис. 6.6. Наклонные струи
Расчет наклонных струй ведут по отношению к величинам  и
и 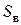 для вертикальных струй.
для вертикальных струй.
Огибающая кривая компактной струи abc мало отличается от дуги окружности, описанной радиусом, который для ручных стволов диаметром насадка не выше 25 мм можно принять равным  т.е.
т.е.
 . (6.16)
. (6.16)
Для насадков больших диаметров, например для лафетных стволов, линия abc более вытянута вдоль горизонтальной оси. Минимальная длина компактных струй, ручных стволов с насадками 13, 16, 19, 22 и 25 мм требует создания напора перед насадком от 30 до 50 м.
Расстояние от насадка до огибающей кривой раздробленной струи (см. рис. 6.3) возрастает с уменьшением угла наклона  к горизонту
к горизонту  . Величину радиуса действия раздробленной струи определяют по формуле
. Величину радиуса действия раздробленной струи определяют по формуле
 , (6.17)
, (6.17)
где  - коэффициент, зависящий от угла наклона
- коэффициент, зависящий от угла наклона  .
.
Значения коэффициента  определены опытным путем и приведены в табл. 6.4.
определены опытным путем и приведены в табл. 6.4.
Таблица 6.4
| q¢, град | |||||||
| b | 1,40 | 1,30 | 1,20 | 1,12 | 1,07 | 1,03 | 1,00 |
Не надо смешивать угол наклона радиуса действия струи  с углом наклона ствола
с углом наклона ствола  . Последний для наклонных струй всегда больше угла наклона
. Последний для наклонных струй всегда больше угла наклона  к горизонту. Например, наибольшая дальность полета струи по горизонтали
к горизонту. Например, наибольшая дальность полета струи по горизонтали  наблюдается при угле наклона ствола
наблюдается при угле наклона ствола  = 30º, при этом коэффициент
= 30º, при этом коэффициент  равен 1,4.
равен 1,4.
Дата добавления: 2014-11-13; просмотров: 2046; Мы поможем в написании вашей работы!; Нарушение авторских прав |