Анализ полученного результата

Полученное выражение позволяет сделать следующий принципиальный вывод.

Если kR<1, то по отношению к таким возмущениям цилиндрическая поверхность струи неустойчива, так как волнообразование энергетически выгодно. Что означает kR<1? Именно то, что неустойчивость будет проявляться в том случае, если длина волны возмущения больше длины окружности.

По отношению к решению задачи этот вывод показывает, что мы правильно предположили, что 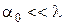. Практический же вывод - для того чтобы получить дальнобойную пожарную струю, необходимо устранить возмущения (длинноволновые) на выходе из насадка (т.е. должны отсутствовать задиры, забоины и т.д.).

Так как возмущения не с любой длиной волны приводят к неустойчивости, то должны существовать возмущения, которые особенно быстро приводят к распаду струи. Для нахождения длины волны таких возмущений проанализируем полную энергию системы, а для этого вначале найдем кинетическую энергию.

6.2.3. Определение кинетической энергии частиц жидкости
в струе, обусловленной их движением под действием
колебаний поверхности

Определим кинетическую энергию частиц жидкости в струе, обусловленную их движением под действием колебаний поверхности. Для этого необходимо получить аналитические выражения для компонент скорости v_r и v_z. Ранее мы отметили, что движение потенциальное и

(*)

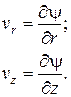
Найдем . Поскольку в выражении для содержится , то в выражении для также должен быть косинус. Будем искать решение дифференциального уравнения в виде:

. (**)

тогда

Подставляя выражение для (**) в уравнение (*), получаем:

.

Мы получили дифференциальное уравнение, исследование которого провел Фридрих Бессель и получил фундаментальную систему решений. (Уравнение Бесселя нулевого порядка). Решение уравнения имеет вид:

,

где - функции Бесселя первого и второго рода нулевого порядка.

при r = 0 (на оси струи) скорость или равна 0 или конечной величине.

Так как при r = 0 , то .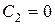

Поэтому решение уравнения (*) имеет вид:

,

где C- постоянная интегрирования - должна быть найдена из дополнительных физических соображений. Для поверхности

- радиальная скорость частиц жидкости, находящихся на поверхности струи

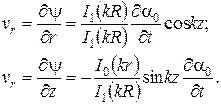
Кинетическая энергия частицы жидкости:

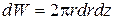
на единицу длины струи .

6.2.4. Определение скорости нарастания колебаний
поверхности струи

Если после наложения возмущения система (струя) предоставлена сама себе и энергия не подводится, то:

С учетом выражений для и получим:

или

Решение будем искать в виде:

; .

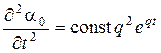Подставляя в исходное уравнение, получаем:

.

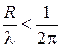Таким образом, если (т.е. ), то 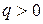и, следовательно, (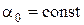 ) будет возрастать по экспоненциальному закону. Это приведет к распаду струи на отдельные капли.

График зависимости для воды имеет вид (рис. 6.2.)

Рис. 6.2. Зависимость

Из графика видно, что = 0,7 и, значит, .

Таким образом, наиболее опасное возмущение (т.е. возмущение, приводящее к наиболее быстрому нарастанию амплитуды колебаний и, следовательно, наиболее быстрому распаду водяной струи) имеет длину волны 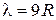(где R - радиус невозмущенной струи).

6.2.5. Влияние вязкости жидкости, сил тяжести,
межфазного трения на разрушение струи

Для реальных струй необходимо учесть вязкость, действие сил тяжести, межфазное трение. Задача сильно усложняется. Кроме того, в реальных струях, как правило, движение непотенциальное (турбулентное). Однако использованный подход к решению задачи об устойчивости реальных струй может быть применен. Учет реальности приводит к некоторому изменению величины , а принципиальные выводы об устойчивости сохраняются.

Длина непрерывной части струи представляет собой расстояние, проходимое струей за время нарастания колебаний до такой степени, что струя распадается ( ). Следовательно, длина непрерывной части зависит от характера возмущений . При устранении возмущений длина компактной струи может быть значительно увеличена. В случае реальных струй увеличение все равно ограничено в связи с действием гравитационной неустойчивости и межфазного трения.

Уравнение энергии для несжимаемых жидкостей:

Учет вязкости можно выполнить следующим образом:

где - работа сил трения в объеме W за время t.

При учете вязкости происходит уменьшение инкремента q колебаний по абсолютной величине и смещение в сторону больших длин волн максимума q. Интервал неустойчивости не меняется (рис. 6.3).

(Можно отметить, что полученные результаты справедливы для малых возмущений и, следовательно, характеризуют их нарастание в начальный период.)

Рис. 6.3. Влияние вязкости жидкости на величину

инкремента колебаний

Таким образом, цилиндрическая поверхность жидких струй неустойчива по отношению к возмущениям определенной длины волны (т.е. происходит распад на капли) и существуют возмущения, приводящие к особенно быстрому распаду струй. Для воды эти возмущения имеют длину волны .