
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теоретический анализ влияния поверхностного натяжения жидкости на устойчивость струи
Предположим, имеется сплошная цилиндрической формы струя идеальной жидкости. Трение на границе раздела фаз отсутствует. Силы тяжести не влияют на характер движения жидкости (т.е. силы тяжести не учитываем). Течение жидкости в струе безвихревое. При сделанных допущениях в системе координат движущейся со скоростью жидкости - жидкость неподвижна.
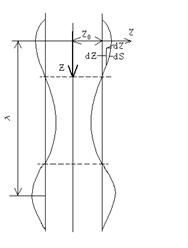
Рис. 6.1. Форма струи
Предположим, что в какой-то момент времени в результате случайного малого возмущения поверхность цилиндрической струи приобрела форму, показанную на рис. 6.1. и описываемую уравнением
 ,
,
где  - волновое число;
- волновое число;  - малая величина, т.е.
- малая величина, т.е.  ;
;  - длина волны возмущения.
- длина волны возмущения.
После такого возмущения поверхность жидкости придет в движение вследствие действия сил поверхностного натяжения (т.е. они стремятся сократить поверхность, но по инерции гребни будут опускаться ниже нейтральной линии и поверхность жидкости придет в колебательное движение). Следовательно, в выбранной нами системе координат жидкость в струе вблизи поверхности также придет в движение.
Предположим, что это движение безвихревое, т.е. потенциальное движение (существует функция  , которая удовлетворяет условию
, которая удовлетворяет условию  , т.е.
, т.е.  ...). В случае потенциального движения, потенциал скорости
...). В случае потенциального движения, потенциал скорости  удовлетворяет уравнению Лапласа, т.е.
удовлетворяет уравнению Лапласа, т.е.
 .
.
Мы рассматриваем осесимметричную задачу. Поэтому решение удобно проводить в цилиндрических координатах. В этих координатах оператор Лапласа, в случае двухмерного движения, имеет вид:
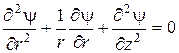

Здесь мы принимаем во внимание тот факт, что движение по углу  (т.е. в касательном направлении к поверхности отсутствует).
(т.е. в касательном направлении к поверхности отсутствует).
Для анализа устойчивости (т.е. будет ли нарастать во времени амплитуда колебаний поверхности или уменьшаться) воспользуемся энергетическим методом. Для этого найдем изменение полной энергии рассматриваемого жидкого тела, которая состоит из потенциальной энергии, обусловленной действием сил поверхностного натяжения, и кинетической энергии движущихся частиц жидкости.
Энергия поверхностного натяжения прямо пропорциональна величине поверхности. Поэтому, для того чтобы найти изменение энергии поверхностного натяжения при искривлении поверхности, необходимо просто найти изменение поверхности.
Величина  не остается абсолютно постоянной во время движения; ее значение должно определяться условием неизменности заключенного в цилиндре объема. Жидкость несжимаема и, следовательно, объем выделенного участка струи постоянен. Будем рассматривать участок струи длиной
не остается абсолютно постоянной во время движения; ее значение должно определяться условием неизменности заключенного в цилиндре объема. Жидкость несжимаема и, следовательно, объем выделенного участка струи постоянен. Будем рассматривать участок струи длиной  .
.
 .
.
Учтем, что  .
.
После интегрирования и подстановки пределов интегрирования получим:
 .
.
С другой стороны,  , где
, где  - радиус невозмущенной поверхности струи. Так как
- радиус невозмущенной поверхности струи. Так как  , то
, то
 ;
;  ;
; 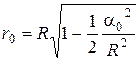 .
.
Участок поверхности  ;
;
 (см. уравнение поверхности)
(см. уравнение поверхности)
 .
.
Непрерывную функцию можно разложить в ряд Маклорена:

Разложим функцию  :
:

Если  , то можно с достаточно высокой точностью ограничиться первыми членами разложения
, то можно с достаточно высокой точностью ограничиться первыми членами разложения
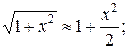
 .
.
Тогда: 


 .
.
Поверхность участка возмущенной струи длиной  равна:
равна:

 .
.
После подстановки пределов интегрирования получим:
 .
.
Так как  , то
, то

так как  .
.
Таким образом, изменение поверхности на участке струи длиной  равно
равно
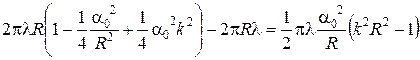
или изменение поверхности на единицу длины
 .
.
Изменение потенциальной энергии при волнообразовании на единицу длины струи равно:
 ;
; 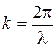 .
.
Если l > 2pR, то  и энергия поверхностного натяжения уменьшится, и при волнообразовании амплитуда колебаний должна расти.
и энергия поверхностного натяжения уменьшится, и при волнообразовании амплитуда колебаний должна расти.
Дата добавления: 2014-11-13; просмотров: 386; Мы поможем в написании вашей работы!; Нарушение авторских прав |