
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ИСТЕЧЕНИЕ ЖИДКОСТИ ИЗ НАСАДКОВ
Насадком называется присоединенная к отверстию в стенке трубка, длина которой составляет три-четыре диаметра. Различают следующие основные типы насадков (рис. 5.4):
цилиндрические (внешние - а и внутренние - б);
конические (сходящиеся - в и расходящиеся - г)
коноидальные (с закругленными очертаниями по форме сжатия струи - д).
Большое влияние на скорость истечения и расход из насадков оказывает форма входной кромки. Например, плавное закругление на входе может полностью устранить внутреннее сжатие струи и вызвать увеличение скорости и расхода.
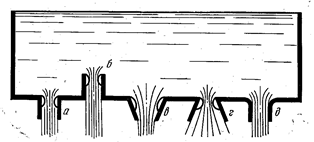
Рис. 5.4. Истечение жидкости через насадки
Внешний цилиндрический насадок (рис. 5.5). Струя жидкости при выходе в насадок сжимается, после чего вновь расширяется и заполняет все сечение насадка. В промежутке между сжатым сечением и стенками насадка образуется вихревая зона. Так как струя выходит из насадка полным сечением (без сжатия), то коэффициент сжатия струи e = 1, а коэффициент расхода m = ej = j, т.е. для насадка коэффициенты расхода и скорости имеют одинаковую величину.
Составляя уравнение Бернулли для сечений I-I и II-II, взятых на свободной поверхности жидкости в сосуде и в месте выхода струи из насадка, и рассуждая точно так же, как и в случае истечения жидкости из отверстия в тонкой стенке, получаем следующие расчетные формулы:
для скорости истечения из насадка
 (5.9)
(5.9)
где  ;
;
для расхода при истечении из насадка
 . (5.10)
. (5.10)
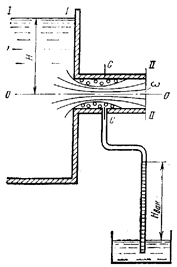 |
Рис. 5.5. Внешний цилиндрический насадок
Коэффициент скорости насадка j можно определить, зная величину коэффициента сопротивления насадка zн. Для этого определим потери напора при истечении жидкости через насадок, которые в данном случае обуславливаются сопротивлением отверстия в тонкой стенке и внезапным расширением струи. Что касается потерь напора по длине насадка, то их величина незначительна и ими можно пренебречь.
Тогда

Подставляя 
получаем  ,
,
где выражение в скобках представляет собой zн.
Зная, что zт.с = 0,06, определим zв.р по формуле (4.42),
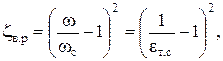
получим  .
.
Таким образом, коэффициент скорости для насадка будет равен
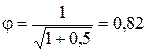 .
.
Следовательно, и коэффициент расхода насадка m = 0,82.
В случае истечение жидкости под уровень формулы для скорости и расхода принимают вид:

где  - разность уровней или напоров воды.
- разность уровней или напоров воды.
Сопоставляя значение коэффициентов истечения для насадков и отверстий в тонкой стенке, видно, что расход жидкости из цилиндрического насадка больше, чем из отверстия в тонкой стенке:
 ,
,
а скорость значительно меньше, чем при истечении из отверстия
 .
.
Внешний цилиндрический насадок, увеличивая расход жидкости, вместе с тем дает и значительное уменьшение скорости истечения. Объясняется это тем, что в вихревой зоне насадка, после того как воздух, отжатый струей, будет увлечен потоком наружу, образуется вакуум. Наличие пониженного давления в области сжатого сечения струи порождает фактор подсасывания жидкости, который оказывает более сильное влияние на расход, чем дополнительное сопротивление вследствие трения по длине и расширения струи в трубке. При значительной длине трубки  эффект подсасывания не компенсирует дополнительных потерь, благодаря чему расход из трубке станет равным или меньше, чем при свободном истечении из отверстия в тонкой стенке. Хотя при этом потери напора растут, их влияние на уменьшение скорости во входном сечении меньше, чем влияние увеличения живого сечения струи.
эффект подсасывания не компенсирует дополнительных потерь, благодаря чему расход из трубке станет равным или меньше, чем при свободном истечении из отверстия в тонкой стенке. Хотя при этом потери напора растут, их влияние на уменьшение скорости во входном сечении меньше, чем влияние увеличения живого сечения струи.
Для определения величины вакуума в сжатом сечении струи (см. рис. 5.5) составим уравнение Бернулли для двух сечений: поверхности воды в сосуде I-I и сжатого сечения С-С:
 .
.
Так как pl - pc есть величина вакуума pвак, Нс = 0; V1 = 0; al = aс = 1, получим
 .
.
Выразим скоростной напор в сжатом сечении через напор перед насадком Н из формулы (5.9):
 ,
,
а из уравнения неразрывности найдем 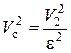 .
.
Тогда  .
.
Подставляя полученное выражение в исходное уравнение, получаем:
 (5.11)
(5.11)
Таким образом, при постоянных параметрах j, ζт.с и ε вакуум в насадке (в сжатом сечении) пропорционален напору.
Подставив числовые значения коэффициента в формулу (5.11), получим значения вакуума при истечении жидкости в атмосферу:
 .
.
Максимальная величина вакуума, равная 10 м, наступает при напоре
 .
.
При понижении абсолютного давления в насадке до давления насыщенных паров возникает кавитационный режим истечения. Выделяющиеся внутри жидкости пары будут заполнять струю, которая начнет терять свою сплошность, в результате уменьшится расход жидкости.
Дальнейшее увеличение напора приводит к отрыву струи жидкости от внутренних стенок насадка (рис. 5.6). При этом понижается коэффициент расхода и, следовательно, пропускная способность насадка. Насадок работает как отверстие в тонкой стенке. Такое явление называется срывом истечения через насадок.
Внутренний цилиндрический насадок (рис. 5.7). В этом насадке явление протекает, как и во внешнем насадке. Однако вследствие большого сжатия струи на входе коэффициенты скорости и расхода для внутреннего насадка меньше, чем внешнего, m = j = 0,71.

Рис. 5.6. Истечение через насадок при срыве
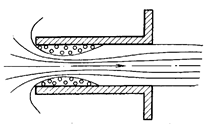
Рис. 5.7. Внутренний цилиндрический насадок
При малой длине внутреннего цилиндрического насадка (l < 1,5d) струя вытекает из него, не касаясь стенок. В этом случае j = 0,98; e = 0,5; m = 0,49.
Гидравлические сопротивления во внутреннем насадке больше, чем во внешнем, следовательно, в нем меньше вакуум и расход жидкости. Поэтому, как правило, внешние насадки предпочитают внутренним, ввиду меньших гидравлических сопротивлений.
Конический сходящийся насадок (рис. 5.8). В коническом сходящемся насадке явление внутреннего сжатия сказывается меньше, чем в цилиндрическом насадке, но зато появляется сжатие струи по выходе из насадка.

Рис. 5.8. Конический сходящийся насадок
Это влечет за собой, с одной стороны, увеличение коэффициента скорости, а с другой - уменьшение коэффициента сжатия. Так как разность между сжатым сечением и расширенной частью струи в коническом сходящемся насадке меньше, чем в цилиндрическом, происходит уменьшение потерь напора на расширение струи и соответственно увеличение расхода. Однако это имеет место до значения угла конусности q = 13º. В последующем вследствие чрезмерного сжатия струи потери возрастают и расход уменьшается.
В среднем при углах конусности 12-14º можно принимать:
e = 0,98; j = 0,96; m = 0,94.
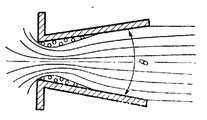
Рис. 5.9. Конический расходящийся насадок
Конический расходящийся насадок (рис. 5.9). Расширение струи в таком насадке происходит более резко, чем в цилиндрическом. Поэтому его гидравлическое сопротивление больше, а коэффициент скорости  меньше. Вследствие того что в расходящемся насадке потери напора от сжатого сечения к расширенному значительно больше, чем в коническом сходящемся и цилиндрическом, происходит снижение коэффициента расхода. Наибольшей пропускной способностью он обладает при углах конусности 6-8º.
меньше. Вследствие того что в расходящемся насадке потери напора от сжатого сечения к расширенному значительно больше, чем в коническом сходящемся и цилиндрическом, происходит снижение коэффициента расхода. Наибольшей пропускной способностью он обладает при углах конусности 6-8º.
Конические расходящиеся насадки (диффузоры) нашли широкое применение в насосах, гидроэлеваторах и т.п., где требуется довести до минимума кинетическую энергию в отходящем потоке.
При угле конусности 5º для конического расходящегося насадка с округленной входной кромкой можно принять  ,
,  .
.
Следует отметить, что этот коэффициент расхода относится к большему (выходному) сечению насадка. Если же отнести этот коэффициент к входному отверстию, то он окажется значительно больше и может достигнуть 2-3.
Коноидальный насадок (см. рис. 5.4, д). Цилиндрический насадок, имеющий плавный вход по форме струи, выходящий из отверстия, называется коноидальным. Истечение жидкости через такой насадок происходит при наименьшем сопротивлении ( 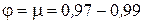 ), что способствует получению дальнобойных струй с большой начальной скоростью полета. Однако из-за сложности изготовления такие насадки в пожарном деле применяются недостаточно широко.
), что способствует получению дальнобойных струй с большой начальной скоростью полета. Однако из-за сложности изготовления такие насадки в пожарном деле применяются недостаточно широко.
Значения коэффициентов для различных отверстий и насадков, отнесенных к выходному сечению, приведены в табл. 5.1
Таблица 5.1
| Тип отверстия или насадка | ζ e j m |
| Круглое отверстие в тонкой | |
| стенке | 0,06 0,64 0,97 0,62 |
| Внешний цилиндрический | |
| насадок | 0,50 1,00 0,82 0,82 |
| Внутренний цилиндрический | |
| насадок | 1,00 1,00 0,71 0,71 |
| Конический сходящийся | |
| насадок q = 13º | 0,09 0,98 0,96 0,94 |
| Конический расходящийся | |
| насадок q = 8º | 3,45 1,00 0,45 0,45 |
| Коноидальный насадок | 0,06 1,00 0,98 0,98 |
Особенности истечения из некруглых отверстий. В зависимости от формы отверстия, через которое происходит истечение, форма поперечного сечения струи имеет самый разнообразный вид (рис. 5.10). Например, поперечное сечение струи, вытекающее через треугольное отверстие, приобретает форму с тремя тонкими ребрами: при истечении через квадратное отверстие - крестообразную и через круглое - эллиптическую. Изменение формы струи происходит под действием сил поверхностного натяжения. Это явление называется инверсией струи. В дальнейшем форма поперечного сечения по длине струи не остается постоянной, она под действием сил поверхностного натяжения все время претерпевает соответствующее изменение. В результате нарушается сплошность струи и она распадается на отдельные капли.

Рис. 5.10. Инверсия струи:
а - форма отверстий; б - форма сечения струи
Исходя из сказанного, следует, что для получения дальнобойных струй необходимо использовать насадки с круглым сечением, в которых действие сил поверхностного натяжения взаимно уравновешивается. Для предохранения выходных кромок насадков от различного рода повреждений предусматриваются специальные кольцевые выточки.
Расчетные формулы для расхода и напора из насадков. Формулу для определения расхода можно представить в виде
 , (5.12)
, (5.12)
где  называется проводимостью насадка.
называется проводимостью насадка.
Напор перед насадком определяется из выражения
 , (5.13)
, (5.13)
где  сопротивление насадка.
сопротивление насадка.
Значение  и
и  насадков при
насадков при  для определения расходов
для определения расходов  , л/с, и напора
, л/с, и напора  , м, для пожарных стволов приводится в табл. 5.2.
, м, для пожарных стволов приводится в табл. 5.2.
Таблица 5.2
| Диаметр насадка, мм s p |
| 13 2,89 0,588 |
| 16 1,26 0,891 |
| 19 0,634 1,26 |
| 22 0,353 1,68 |
| 25 0,212 2,17 |
| 28 0,135 2,72 |
| 32 0,079 3,56 |
| 38 0,04 5,00 |
| 50 0,013 8,77 |
| 65 0,004 14,74 |
Дата добавления: 2014-11-13; просмотров: 2485; Мы поможем в написании вашей работы!; Нарушение авторских прав |