ДАВЛЕНИЕ СТРУИ

Рассмотрим динамические свойства компактной струи, вытекающей из насадка. На рис. 6.7, а показан случай удара струи о твердую преграду такой формы, при которой жидкость на поверхности растекается двумя потоками под углам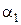и и 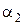к оси струи. При этом преграда испытывает воздействие силы давления струи P в направлении от насадка, вызывающее, согласно закону Ньютона, ответную силу реакции R, которая равна по величине, но противоположна по знаку силе P. Массу жидкости и среднюю скорость в сечении основной струи обозначим соответствено 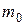и 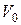, а в растекающихся потоках и .

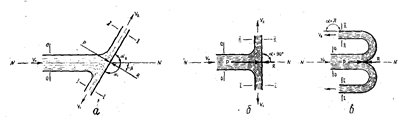
Рис. 6.7. Давление струи на преграду:

а - произвольно расположенная плоская преграда;

б - нормальная плоская преграда;

в - криволинейная симметричная преграда

Используя теорему количества движения к объему жидкости, заключенному между нормальными сечениями 0-0, I-I, II-II относительно оси N-N, получим:

. (6.19)

Решая это уравнение относительно R, получаем:

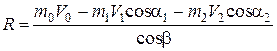. (6.20)

Выражение (6.20) можно использовать для определения силы давления при ударе струи жидкости о плоскую неподвижную преграду. Наиболее простым случаем является нормальный удар, показанный на рис. 6.7, б, при котором направление реактивной силы R совпадает с осью N-N, , ,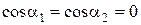

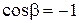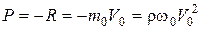, (6.21)

где - живое сечение набегающей струи.

Сила удара значительно повышается, если струя воздействует на поверхность, для которой 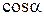является отрицательным.

В случае криволинейных симметричных поверхностей (рис. 6.7, в), для которых углы 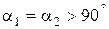и 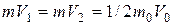, в соответствии с формулой (6.21), получим:

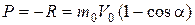. (6.22)

Если угол 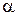довести до значения a = 180º, то сила давления на поверхность достигнет максимума:

. (6.23)

Обычно по типу с углом 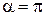выполняются лопатки рабочего колеса современных турбин, что обеспечивает максимальное использование кинетической энергии потоков.