УРАВНЕНИЕ БЕРНУЛЛИ ДЛЯ НЕУСТАНОВИВШЕГОСЯ ДВИЖЕНИЯ

Неустановшимся (нестационарным) называют такое движение жидкости, при котором скорость, давление в отдельных точках пространства, заполненного движущейся жидкостью, с течением времени изменяются и, следовательно, и . С неустановившимся движением жидкости встречаемся на практике при быстром включении и выключении подачи жидкости в стационарные установки пожаротушения, при открытии и закрытии пожарных гидрантов, задвижек на водопроводной сети, при включении и выключении насосов, при быстром вскрытии распылителя в быстродействующей системе пожаротушения, в момент начала и прекращения подачи воды по пожарным рукавам и т.д.

Уравнение Бернулли для неустановившегося движения можно получить из уравнения Эйлера для элементарной струйки идеальной жидкости.

Рассмотрим участок элементарной струйки длиной ds в поле силы тяжести (рис. 7.1).

Рис. 7.1. К выводу уравнения Бернулли

для неустановившегося движения

Так как площадь поперечного сечения dw элементарной струйки бесконечно мала, то величины скорости и давления для всех точек данного поперечного сечения в данный момент времени одинаковы; вдоль струйки эти величины могут изменяться. Тогда уравнение Эйлера принимает вид:

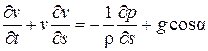, (7.1)

где gcosa - проекция единичной массовой силы на направление движения (ось S),

.

Если бы мы выбрали струйку, наклоненную не вниз, а вверх, то , но сама проекция единичной массовой силы g на направление движения была бы отрицательной. Таким образом, выбор наклона струйки не снижает общности рассуждений.

С учетом того, что

уравнение Эйлера (7.1) можно записать так:

или . (7.2)

Умножая уравнение (7.2) на ds и интегрируя его от сечения с координатой s₁ до сечения элементарной струйки с координатой s₂, получим известное по предыдущим разделам курса уравнение Бернулли, дополненное одним новым членом:

или (7.3)

, (7.4)

h_ин - имеет размерность длины, учитывает силы инерции и называется инерционным напором.

Таким образом, члены уравнения (7.3) представляют сумму
геометрического, пьезометрического, скоростного и инерционного
напоров.

Уравнение Бернулли относится к некоторому определенному моменту
времени. Поэтому все члены уравнения должны вычисляться для одного
и того же момента времени.

Переходя к рассмотрению потока реальной (вязкой) жидкости, необходимо учесть потери напора, обусловленные диссипацией механической энергии. Уравнение Бернулли для потока реальной жидкости имеет вид:

, (7.5)

где 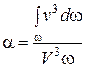- коэффициент кинетической энергии, характеризующий отношение действительной величины кинетической энергии массы жидкости, проходящей через рассматриваемое сечение, к кинетической энергии, определенной по средней скорости.

- инерционный напор;

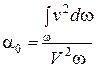- коэффициент количества движения, представляющий отношение действительной величины количества движения массы жидкости к величине количества движения ее, подсчитанной по средней скорости. Коэффициенты a и a₀ всегда больше единице. Однако при турбулентном режиме движения эти коэффициенты близки к единице (1,02 - 1,16) и для практических расчетов полагают a = 1 и a_o = 1; h_1-2 - потери напора.

Отметим, что если ускорение постоянно на всем отрезке l = s₂ -s₁ и равно a, то инерционный напор:

(7.6)