Расчет газопроводов при больших перепадах давления

При расчете длинных газопроводов и при высоких скоростях течения газа имеют место значительные перепады давления ( 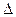p/p_cр > 0,05). В этом случае наблюдается заметное изменение плотности движущегося газа, что приводит даже при постоянном сечении трубопровода к возрастанию скорости течения к концу газопровода. Такая ситуация бывает в установках газового пожаротушения.

Исходным уравнением для расчета газопроводов будет уравнение Бернулли в дифференциальной форме (8.2), в которой введены средняя скорость и член, учитывающий линейные потери:

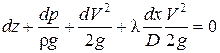. (8.14)

Здесь dх - бесконечно малой длины участок трубопровода, D - внутренний диаметр трубопровода.

Рассмотрим случай, когда изменением Z и скоростного напора можно пренебречь.

Тогда:

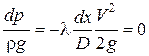. (8.15)

В соответствии с уравнением (8.1)

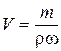. (8.16)

Подставляя уравнение (8.16) в уравнение (8.15), получаем:

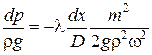
или 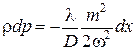. (8.17)

При политропическом процессе изменения состояния газа с учетом уравнения (8.6) будем иметь:

Рассмотрим случай, когда линейный коэффициент гидравлического сопротивления вдоль трубопровода имеет одно и то же значение.

Интегрируя в пределах от p₁ до p₂ (где p₂ - давление в конце трубопровода длиной l) и от 0 до l, получим:

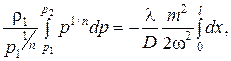
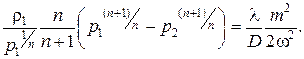
С учетом того, что 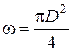, после преобразований выражение для массового расхода газа примет вид:

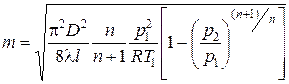. (8.18)

Если трубопровод имеет тепловую изоляцию, то показатель политропы следует заменить на показатель адиабаты (n = k).

Для трубопроводов без тепловой изоляции при наличии теплообмена между газом и окружающей средой температура газа может практически сохраняться постоянной по всей длине газопровода, равной температуре окружающей среды.

Учитывая связь между кинематической и динамической вязкостью (1.12), число Рейнольдса можно записать:

.

Как следует из разд. 1.1 при постоянной температуре динамическая вязкость сохраняется неизменной. Из уравнения неразрывности (8.1) следует, что произведение rV = const для трубопровода постоянного сечения, следовательно, при изотермическом процессе остается постоянным и число Рейнольдса. А это значит, что величина коэффициента гидравлического трения остается постоянной.

Таким образом, предположение, что l = const точно выполняется только для изотермического течения газа.

Для изотермического процесса n = 1 и формулу (8.18) можно привести к виду:

. (8.19)

Таким образом, расчет газопроводов при больших перепадах давления сводится обычно к определению их пропускной способности и формулы (8.18) и (8.19) - основные расчетные формулы для определения массового расхода при заданных диаметре трубопровода и перепаде давления. Эти формулы могут служить также и для определения диаметра трубопровода при заданном массовом расходе газа и перепаде давления.

При дозвуковых скоростях течения линейный коэффициент гидравлического сопротивления можно определить по формулам (4.34) – (4.37 ) для капельной жидкости.

Например, в случае ламинарного режима движения:

.

Если течение изотермическое, то формулу (8.19) можно преобразовать следующим образом:

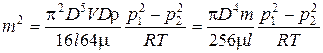
или 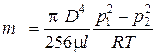. (8.20)

Подчеркнем, что формула (8.20) справедлива только для ламинарного режима движения при постоянной температуре газа.