
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Уравнение неразрывности и уравнение Бернулли для газа
Перекачка по трубам газов имеет весьма широкое применение, в том числе и в установках газового пожаротушения. По сравнению с движением жидкостей движение газов характеризуется рядом особенностей, обусловленных различием физических свойств жидкостей и газов, сжимаемостью газов.
Так как при изменении давления плотность газа меняется существенно, то уравнение неразрывности (2.11) должно использоваться для массового расхода жидкости
 , (8.1)
, (8.1)
т.е. масса газа, протекающего в единицу времени через любое живое сечение потока (или элементарной струйки), постоянна.
При выводе уравнения Бернулли для элементарной струйки идеальной жидкости было получено:
 .
.
Для газов плотность вносить под знак дифференциала нельзя, так как при течении сжимаемого газа надо учитывать r = f(p). При движении реальных газов, обладающих вязкостью, следует учитывать потери напора и уравнение Бернулли примет вид:
 . (8.2)
. (8.2)
Интегрируя уравнение (8.2) по длине от некоторого сечения I-I до сечения II-II, получим:
 . (8.3)
. (8.3)
Уравнение состояния газа выражает зависимость между абсолютным давлением p, плотностью r и абсолютной температурой T:
 , (8.4)
, (8.4)
где R - газовая постоянная, равная универсальной газовой постоянной
R = 8314 Дж/(кмоль×град), поделенной на массу M одного киломоля данного вещества
 , Дж/(кг×град). (8.5)
, Дж/(кг×град). (8.5)
Значения газовой постоянной для некоторых веществ приведены в табл. 8.1.
При политропическом процессе 
или  . (8.6)
. (8.6)
Таблица 8.1
| Вещество | Химическая формула | R, Дж/(кг×град) |
| Водяной пар | Н2О | 461,5 |
| Азот | N2 | 296,8 |
| Двуокись углерода | СО2 | 189,9 |
| Окись углерода | СО | 296,8 |
| Воздух | 287,0 |
Подставляя уравнение (8.6) в уравнение (8.3), после преобразований получаем:
 . (8.7)
. (8.7)
В уравнении (8.7) величина  называется температурным напором.
называется температурным напором.
Таким образом, в установившемся движении газа величина полного напора равна сумме геометрического, пьезометрического, скоростного и температурного напоров.
При адиабатическом процессе (нет теплообмена) в уравнении (8.7) вместо показателя политропы n следует подставить показатель адиабаты k.
Если температура газа при течении не меняется (изотермический процесс, Т = const),то из уравнения (8.4) следует:
 ,
,
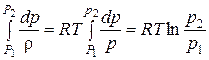
и уравнение Бернулли примет вид:
 .
.
Дата добавления: 2014-11-13; просмотров: 438; Мы поможем в написании вашей работы!; Нарушение авторских прав |