ЗАТОПЛЕННЫЕ СТРУИ

Затопленные свободные струи наблюдаются, например, при подаче или отсасывании масс воздуха из помещения, при истечении газа из насадка в воздушную среду, при выходе в водоем трубопровода, заглубленного под уровень, при истечении жидкости через затопленное отверстие и т.п.

Наблюдения показывают, что струя, вытекающая в массу однородной жидкости, постепенно расширяется и на некотором расстоянии от насадка рассеивается в ней. Рассеивание струи обуславливается действием турбулентного обмена между струей и окружающей ее жидкостью.

На границе между струей и неподвижной жидкостью вследствие вязкости образуются вихри. Эти вихри, затормаживая движение струи, способствуют увеличению ее массы, увлекая в движение жидкость извне. На место частиц, выброшенных из струи, в нее проникают частицы, увлеченные струей из окружающей жидкости, которые подтормаживают граничные слои струи.

Слой, в котором происходит перемешивание основной массы струи и окружающей ее неподвижной массы, называют турбулентным слоем.

С внешней стороны пограничный слой струи соприкасается с неподвижной жидкостью, с внутренней - с ядром струи, скорость в котором постоянная (рис. 6.14.)

Рис. 6.14. Схема затопленной свободной струи

По мере утолщения пограничного слоя сужается ядро струи. На некотором расстоянии от выхода струи ядро исчезает и вся струя охватывается пограничным слоем.

Сечение струи, в котором завершается ликвидация ядра, называется переходным, а участки струи, расположенные до переходного сечения и после него, называют соответственно начальным и основным.

Опыты показывают, что границы струи очерчиваются прямыми линиями и образуют угол, равный примерно 28°. Точка пересечения границ струи называется полюсом струи.

Рассмотрим теперь, как изменяется скорость на оси основного участка струи. А.Я. Милович впервые установил на основании опытов с газовыми струями, что осевая скорость на основном участке осесимметричной струи изменяется вдоль струи по гиперболической зависимости.

, (6.33)

где - осевая скорость в сечении, отстоящем от начального на расстоянии 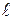; - опытный коэффициент; 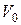- скорость в начальном сечении струи; 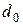- диаметр струи в начальном сечении.

Коэффициент j определяется по формуле, предложенной Г.Н. Абрамовичем:

. (6.34)

На начальном участке до переходного сечения осевая скорость равна скорости истечения, т.е. 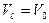. Тогда длина начального участка равна

.

Диаметр струи в сечении, взятом на расстоянии от насадка, определим по формуле Г.Н. Абрамовича:

.

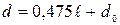В.М. Коновалов исследовал водяные струи, вытекающие из насадка в пространство, занятое водой, находящейся в неподвижном состоянии. Для определения он получил формулу тождественную с формулой (6.33), в которой

. (6.35)

Исследованиями В.Я. Чичасова, проводимыми с гидравлическими струями, вытекающими из насадков в поток жидкости, установлено, что при совпадении направлений движения струи и потока струя практически исчезает (рассеивается) на расстоянии от насадка .

Таким образом, было определено, что для затопленных струй (газовых и водяных) применимы одни и те же уравнения, отличие будет только в определении экспериментальных констант, входящих в уравнения.