КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Взаимодействие фотонного излучения с веществом
При решении ряда задач о прохождении фотонного ионизирующего излучения через вещество достаточно использовать закон ослабления узкого пучка моноэнергетического фотонного излучения:
, (3.1)
где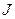 
− поток фотонов, k − линейный коэффициент ослабления для фотонов, 
− толщина слоя вещества. Часто вводится массовый коэффициент ослабления µ = k/r, где r − средняя плотность вещества; в этом случае толщину ослабляющей среды определяют как d = rx. Для основных процессов взаимодействия фотонов с веществом (фотоэффект, ph; Комптон-эффект, c; образование электрон-позитронных пар, pp) µ описывается формулой
, (3.2)
где M – средняя молярная масса вещества.
Комптон-эффект − упругое рассеяние фотона на первоначально покоящейся свободной частице (электроне).
Пусть фотон с длиной волны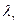 
рассеивается под углом 
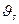на покоящейся частице массой 
. При этом длина волны рассеянного фотона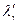 
, а электрон отдачи вылетает под углом 
к направлению распространения падающего фотона. Изменение длины волны фотона при комптоновском рассеянии.
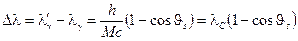, (3.3)
где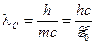 
– комптоновская длина волны частицы с массой 
. (Для электрона комптоновская длина волны 
м, для протона 
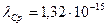м.)
Энергия рассеянного фотона равна
(3.4)
Энергию электрона отдачи (частицы отдачи) можно выразить угол ее рассеяния :
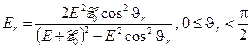(3.5)
Из формул (3.3) и (3.4) следует, что изменение длины волны фотона при комптоновском рассеянии не зависит от самой длины волны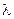 
(и соответственно, энергии 
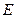) падающего фотона, а определяется только углом рассеяния фотона 
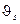. Фотоны рассеянные на углы 
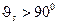, всегда имеют энергию 
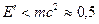МэВ независимо от начальной энергии 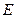, а при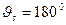 
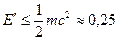МэВ.
Если ввести безразмерные величины 
, 
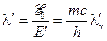и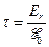 
, то формулы (4) и (5) можно преобразовать к виду:
, ( 
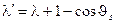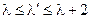), (3.6)
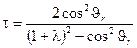. (3.7)
Связь между углами рассеяния задается формулой
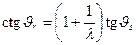. (3.8)
Сечение комптоновского рассеяния описывается формулой Клейна-Нишины:
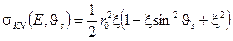, (3.9)
где 
− т.н. классический радиус частицы с зарядом 
и массой , 
.
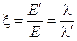Полное сечение комптоновского рассеяния на всем атоме с порядковым номером 
в приближении модели свободных электронов:
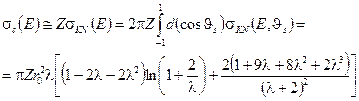(3.10)
Дата добавления: 2015-04-15; просмотров: 157; Мы поможем в написании вашей работы!; Нарушение авторских прав |