
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Фотоэлектрический эффект
При атомном фотоэффекте происходит поглощение фотона атомом, испускание электрона с кинетической энергией, равной в силу закона сохранения энергии
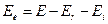 , (3.13)
, (3.13)
где 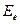 − энергия электрона, вылетевшего из атома;
− энергия электрона, вылетевшего из атома; 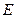 − энергия падающего фотона;
− энергия падающего фотона; 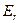 − энергия атома отдачи;
− энергия атома отдачи; 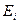 − энергия ионизации (энергия связи электрона в атоме).
− энергия ионизации (энергия связи электрона в атоме).
Поведение сечения фотоэффекта в зависимости от энергии падающих фотонов и порядкового номера атома во многих случаях может быть описано зависимостью
 , (3.14)
, (3.14)
где Z – порядковый номер ядер вещества.
Образование пар в поле ядра (электрона) происходит при взаимодействии налетающего фотона с виртуальным фотоном сильного электростатического поля вблизи ядра или электрона атома. Реакция является эндоэнергетической, и имеет пороговую энергию, практически равную сумме энергий покоя электрона и позитрона 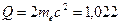 МэВ. (При образовании пар в поле электрона пороговая энергия равна
МэВ. (При образовании пар в поле электрона пороговая энергия равна 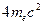 .)
.)
Сечение реакции образования пар в поле ядра с порядковым номером Z в первом приближении: 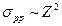 .
.
Задачи
- Какой толщины следует взять алюминиевую пластинку, чтобы она ослабляла узкий пучок рентгеновского излучения с энергией
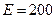 кэВ в такой же степени, как свинцовая пластинка толщиной
кэВ в такой же степени, как свинцовая пластинка толщиной 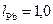 мм?
мм? - Степени ослабления узких пучков рентгеновского излучения с энергиями
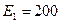 кэВ и
кэВ и  кэВ при прохождении свинцовой пластинки отличаются друг от друга в 4 раза. Найти толщину пластинки и степень ослабления пучка с энергией
кэВ при прохождении свинцовой пластинки отличаются друг от друга в 4 раза. Найти толщину пластинки и степень ослабления пучка с энергией 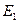 .
. - Вычислить толщину слоя половинного ослабления узкого пучка рентгеновского излучения с длиной волны
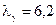 пм для свинца, воды и воздуха.
пм для свинца, воды и воздуха. - Сколько слоев половинного ослабления в пластинке, ослабляющей пучок моноэнергетического рентгеновского излучения в
 раз?
раз? - Для длинноволнового рентгеновского излучения дифференциальное сечение рассеяния фотона на свободном электроне описывается формулой:
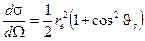 , где
, где 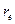 − классический радиус электрона;
− классический радиус электрона; 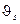 − угол рассеяния фотонов. Найти с помощью этой формулы: а) полное сечение рассеяния; б) относительное число фотонов, рассеянных под углами
− угол рассеяния фотонов. Найти с помощью этой формулы: а) полное сечение рассеяния; б) относительное число фотонов, рассеянных под углами 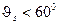 ; в) относительное число электронов отдачи, вылетающих в интервале углов
; в) относительное число электронов отдачи, вылетающих в интервале углов  .
. - Вычислить массовый и линейный коэффициенты рассеяния низкоэнергетического рентгеновского излучения для неона и кислорода при нормальных условиях. Иметь в виду, что атомный коэффициент рассеяния определяется формулой Томсона:
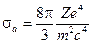 , см2/атом.
, см2/атом. - Точечный источник
 -квантов с энергией
-квантов с энергией 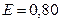 МэВ помещен в центр сферического слоя свинца, толщина которого
МэВ помещен в центр сферического слоя свинца, толщина которого 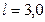 см и внешний радиус
см и внешний радиус 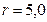 см. Найти плотность потока нерассеянных
см. Найти плотность потока нерассеянных  -квантов на внешней поверхности этого слоя, если активность источника
-квантов на внешней поверхности этого слоя, если активность источника 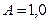 мКи, причем на каждый распад испускается один квант.
мКи, причем на каждый распад испускается один квант. - Узкий пучок
 -квантов, содержащий в одинаковом количестве кванты с энергиями
-квантов, содержащий в одинаковом количестве кванты с энергиями  МэВ и
МэВ и 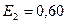 МэВ, падает нормально на свинцовую пластинку толщиной
МэВ, падает нормально на свинцовую пластинку толщиной 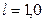 см. Найти отношение интенсивностей обеих компонент пучка после прохождения этой пластинки.
см. Найти отношение интенсивностей обеих компонент пучка после прохождения этой пластинки. - Узкий пучок
 -излучения, содержащий кванты всех энергий в интервале
-излучения, содержащий кванты всех энергий в интервале  МэВ, падает на алюминиевую пластинку толщиной
МэВ, падает на алюминиевую пластинку толщиной  см. Найти степень ослабления интенсивности пучка после прохождения пластинки, если в этом интервале коэффициент ослабления линейно зависит от энергии квантов и спектральная интенсивность падающего излучения не зависит от частоты.
см. Найти степень ослабления интенсивности пучка после прохождения пластинки, если в этом интервале коэффициент ослабления линейно зависит от энергии квантов и спектральная интенсивность падающего излучения не зависит от частоты. - Определить среднюю длину свободного пробега
 -квантов в среде, слой половинного ослабления которой равен
-квантов в среде, слой половинного ослабления которой равен 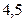 см.
см. - Используя формулу полного сечения комптоновского рассеяния
 -кванта (3.10), вычислить: а) линейный коэффициент комптоновского рассеяния
-кванта (3.10), вычислить: а) линейный коэффициент комптоновского рассеяния  -квантов с энергией
-квантов с энергией 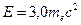 для бериллия; б) массовый коэффициент комптоновского рассеяния
для бериллия; б) массовый коэффициент комптоновского рассеяния  -квантов с энергией
-квантов с энергией  для легких веществ.
для легких веществ. - Тонкую свинцовую пластинку облучали в камере Вильсона
 -квантами с энергией
-квантами с энергией  МэВ. При этом было обнаружено, что электронных треков в
МэВ. При этом было обнаружено, что электронных треков в  раза больше, чем позитронных. Найти отношение вероятности образования электронно-позитронной пары к суммарной вероятности других процессов в этом случае.
раза больше, чем позитронных. Найти отношение вероятности образования электронно-позитронной пары к суммарной вероятности других процессов в этом случае. - Получить выражение, определяющее пороговую энергию
 -кванта для образования электронно-позитронной пары в поле ядра массой
-кванта для образования электронно-позитронной пары в поле ядра массой  .
. - Показать, что
 -квант не может образовать электронно-позитронную пару вне поля ядра, даже если такой процесс энергетически возможен.
-квант не может образовать электронно-позитронную пару вне поля ядра, даже если такой процесс энергетически возможен. - Определить суммарную кинетическую энергию пары электрон-позитрон, которую образует
 -квант с пороговым значением энергии в поле покоящегося протона.
-квант с пороговым значением энергии в поле покоящегося протона.
Дата добавления: 2015-04-15; просмотров: 572; Мы поможем в написании вашей работы!; Нарушение авторских прав |