
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Описание метода. Накачаем в баллон объемом V0 газ и будем «стравливать» его в атмосферу через капилляр диаметром d и длиной L
Накачаем в баллон объемом V0 газ и будем «стравливать» его в атмосферу через капилляр диаметром d и длиной L. Если разность давления Р внутри сосуда и атмосферного давления Р0 достаточно мала, (Р–Р0) << Р0, и течение газа в капилляре ламинарное (слоистое), то расход газа определяется через его вязкость η, перепад давлений на концах капилляра, геометрическими размерами капилляра и описывается формулой Пуазейля:

а падение давления в баллоне описывается изотермическим процессом с убывающей массой газа:

При небольших перепадах давления можно заменить Р на среднее за время наблюдения значение давления газа в баллоне <Р>, а V = V0 . В результате получим

 ,
,
откуда следует, что перепад давлений: ΔP = P – P0 убывает по экспоненте с постоянной времени  :
:
 .
.
Угловой коэффициент графика зависимости 1n(ΔР) от времени даст значение τ, по которому можно найти вязкость:
 . (8.3)
. (8.3)
Если температура T газа в капилляре отличается от температуры Т0 газа в баллоне, то объем прошедшего через капилляр газа равен  и расчетная формула для вязкости
и расчетная формула для вязкости
 . (8.4)
. (8.4)
При больших значениях ΔР течение газа будет турбулентным (при поступательном движении происходит перемешивание слоев газа). Зависимость 1n(ΔР) от времени также оказывается линейной, но с меньшим наклоном. По излому графика можно опознать изменение типа течения. Критерием типа течения является значение числа Рейнольдса
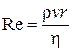 ,
,
где r - радиус капилляра, v - средняя скорость газа, ρ- плотность газа (при нормальных условиях ρвозд = 1,3 кг/м3). Течение в трубе ламинарное при Re < 1000. Поскольку  имеем
имеем
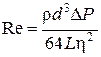 .
.
При d = 0,28 мм и L = 30 мм получим Re ~ 1000 при ΔP ~ 100÷150 мм рт.ст. Эта оценка показывает, что течение воздуха в капилляре будет ламинарным при избыточном давлении в баллоне в несколько десятков мм рт.ст. Тогда в формулах (8.3) и (8.4) можно принять в качестве <P> значение давления на 40 – 60 мм рт.ст. больше атмосферного, т.е. <P> = 800 мм рт.ст. А критическое значение числа Рейнольдса:
 . (8.5)
. (8.5)
Критическое давление определяется в эксперименте по излому графика как давление в точке, находящейся левее пересечения прямых для турбулентного и ламинарного режимов истечения воздуха из капилляра (см. рис.8.2).

Порядок выполнения работы
1. Подключите баллон с двумя штуцерами к груше-помпе при помощи шланга, свободный конец которого выведен из пластмассовой коробки на установке (второй шланг уже подсоединен к штуцеру Ш1).
2. Перекройте кран К1.
3. К штуцеру Ш2 присоедините посредством длинного шланга дроссель-капилляр. К другому концу капилляра подсоедините еще один шланг и опустите капилляр в воду в чайнике на глубину несколько сантиметров, продев шланг в отверстие в крышке чайника, а второй шланг выведите в воздух через носик чайника как показано схематически на рис.8.3.

Вода играет роль термостата, поддерживая температуру капилляра и проходящего через него воздуха равной собственной температуре, а во втором опыте (см. пп. 9,10) обеспечивает подвод тепла к капилляру и проходящему через него воздуху.
4. Измерьте температуру воды в чайнике при помощи термометра.
5. Накачайте в баллон воздух до давления 200-220 мм рт.ст., после чего перекройте зажимом шланг груши-помпы.
6. Подождите 2-3 минуты. При необходимости скорректируйте начальное давление (добавьте воздух грушей или стравите воздух через штуцер Ш2, слегка приоткрывая кран К1).
7. Откройте кран К1 и снимите зависимость давления в баллоне от времени. Для этого нужно:
· поставить часы в режим секунд кнопкой « · »;
· при подходе давления к выбранному значению ΔPнач (160 мм рт.ст.) включить секундомер кнопкой « ◄ »;
· при достижении заданных значений ΔP зафиксировать показания кнопкой « ► », прочесть, записать показания, снова нажать « ► ».
8. Удобные значения приведены в таблице контрольных результатов.
9. Для определения зависимости вязкости воздуха от температуры нужно вскипятить чайник. Включите его, через 2-3 минуты начните, пока чайник еще не закипел, накачивать воздух в баллон как в пп.5,6. К моменту начала проведения повторного опыта чайник должен вскипеть. Температуру воды можно принять равной 100 °С.
10. Снова выполнить пп. 7,8.
11. Постройте графики зависимости ln(∆P) = f (t). Выделите линейные участки и определите постоянные времени tТ и tЛ , для турбулентного и ламинарного режимов течения

У к а з а н и е. Рекомендуемый масштаб: 10 сек в 1 см и 0,1 единицы в 1 см для ln(ΔP). Графики для обоих случаев можно построить на одной координатной сетке.
12. По значению τ для ламинарного течения определите вязкости газа h по фор-мулам (8.3) и (8.4). Определите также из графиков для каждого случая ΔPкрит и рассчитайте критические значения чисел Рейнольдса по формуле (8.5).
При проведении вычислений не забывайте переводить все величины в единицы системы СИ !
13. Результаты оформить в виде предложенной таблицы.
Контрольные результаты
Таблица 8.1. Капилляр: d = 0,28 мм, L = 30 мм. Баллон: V0 = 2,0 л
| ΔP, мм рт.ст. | ln(ΔP) | T0 = ____ , К | T = ____ , К | ||
| t, мин-с | t,c | t, мин-с | t,c | ||
| Пост. времени | t =_____с | t =_____с | |||
| Вязкость возд. | h =_____мкПа×с | h =_____мкПа×с | |||
| Критич. давление | ΔPкрит =_____мм рт.ст. | ΔPкрит =_____мм рт.ст. | |||
| Reкритич |
14.Ответить на следующие контрольные вопросы:
1. Что такое вязкость жидкости? Объясните возникновение сил вязкости с молекулярно – кинетической точки зрения.
2. Каков физический смысл коэффициента динамической вязкости? Пользуясь формулой (8.2), выведите единицы измерения кинематической вязкости.
3. Что называется градиентом скорости?
4. Метод определения коэффициента динамической вязкости.
ЛАБОРАТОРНАЯ РАБОТА №9
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЯЗКОСТИ ЖИДКОСТИ МЕТОДОМ СТОКСА
Цель работы: ознакомиться с методом и определить коэффициент вязкости предложенной жидкости.
Приборы и принадлежности: стеклянный цилиндр с исследуемой жидкостью, металлические шарики, микрометр, секундомер, миллиметровая линейка.
Описание метода
Силами внутреннего трения в жидкости обусловлено сопротивление, которое испытывает твердое тело при движении относительно жидкости. Аналитическое решение задачи нахождения силы сопротивления является очень сложным. Подобная задача была решена английским физиком Стоксом лишь для случая очень медленного движения шарика в безграничном объеме жидкости. Сила сопротивления в этом случае оказалась равной следующей величине:
 , (9.1)
, (9.1)
здесь r- радиус шарика; v - его скорость относительно части жидкости, находящейся в покое.
 Формула Стокса (9.1) позволяет определить коэффициент вязкости h, если известны другие величины. Метод определения коэффициентавязкости с помощью уравнения (9.1) называется методом Стокса.
Формула Стокса (9.1) позволяет определить коэффициент вязкости h, если известны другие величины. Метод определения коэффициентавязкости с помощью уравнения (9.1) называется методом Стокса.
Рассмотрим медленное падение шарика в вязкой жидкости. При движении шарика слой жидкости, граничащий с его поверхностью, прилипает к шарику и движется со скоростью шарика. При вычислении сопротивления среды следует учитывать трение отдельных слоев жидкости друг о друга, а не трение шарика о жидкость.
На шарик, падающий в вязкой жидкости, действуюттри силы(рис.9.1):
1) сила тяжести:  ;
;
2) сила Архимеда:  , равная весу жидкости в объёме шарика;
, равная весу жидкости в объёме шарика;
3) сила сопротивления:  , обусловленная вязкостью жидкости,
, обусловленная вязкостью жидкости,
где r - плотность материала шарика; rж - плотность жидкости;
g - ускорение свободного падения; V - объем шарика;
Все три силы направлены по вертикали: F1 - вниз, F2 и F3 - вверх.
В общем случае уравнение движения шарика имеет вид:
 . (9.2)
. (9.2)
Сила сопротивления с увеличением скорости движения шарика возрастает, а ускорение, dv/dt уменьшается до тех пор, пока шарик не достигнет такой скорости n0, при которой ускорение равно 0. Тогда уравнение (9.2) примет вид:
 . (9.3)
. (9.3)
В этом случае шарик движется с постоянной скоростью n0.
Решая (9.3) относительно h, получим
 . (9.4)
. (9.4)
Если теперь учесть, что  ,
,  ,
,  , где d - диаметр шарика; l - длина участка равномерного движения, пройденного за время t, то формула (9.4) примет окончательный вид:
, где d - диаметр шарика; l - длина участка равномерного движения, пройденного за время t, то формула (9.4) примет окончательный вид:
 . (9.5)
. (9.5)
Таким образом, для нахождения h нужно измерить d, l и t.
Дата добавления: 2014-10-31; просмотров: 341; Мы поможем в написании вашей работы!; Нарушение авторских прав |