Теоретические сведения. Механические колебания - это многократно повторяющиеся движения тела, т.е

Механические колебания - это многократно повторяющиеся движения тела, т.е. движения, при которых тело периодически (через равные промежутки времени) проходит через одно и то же положение в одном и том же направлении.

Простейшими и в то же время часто встречающимися являются гармонические колебания - такие колебания, которые происходят по закону синуса (косинуса).

В зависимости от характера воздействия, оказываемого на колеблющуюся систему, различают свободные (собственные) колебания, вынужденные колебания, автоколебания и другие. Рассмотрим свободные колебания.

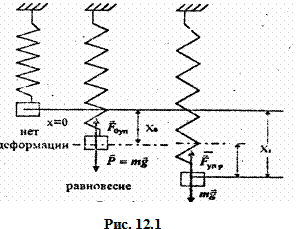
Свободными называются колебания, которые происходят в системе, предоставленной самой себе, после того, как она однажды была выведена из положения равновесия. Различают незатухающие и затухающие свободные колебания, хотя, строго говоря, незатухающих свободных колебаний в природе не бывает. Рассмотрим свободные колебания на примере пружинного маятника, представляющего собой тело (материальную точку), подвешенное на пружине (рис. 12.1).

В состоянии равновесия сила тяжести тела Р = m g (m - масса тела, g - ускорение свободного падения) уравновешивается упругой силой, действующей на тело со стороны пружины (k - коэффициент жесткости пружины, x₀ - равновесное удлинение пружины).

Таким образом,

(12.1)

Если тело вывести из состояния равновесия (например, оттянуть вниз), а затем отпустить, то оно начнет колебаться. Это и есть свободные колебания. Выясним характер этих колебаний, пренебрегая пока силами трения.

На колеблющееся тело по-прежнему действуют сила тяжести mg и упругая сила , где x₁- общее удлинение пружины (см. рис.12.1), разное для различных моментов времени. Знак минус указывает на то, что упругая сила направлена в сторону, противоположную смещению. Следовательно, уравнение движения запишется так:

(12.2)

Или, учитывая равенство (12.1),

(12.3)

Обозначив 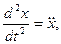х₁-х₀ = х - смещение тела от положений равновесия перепишем выражение (12.3) в виде

или 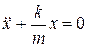(12.4)

k и т - величины сугубо положительные, поэтому их отношение можно представить в виде квадрата некоторого числа , тогда уравнение (12.4) запишется как

(12.5)

Решение уравнения (12.5) имеет вид

(12.6)

Выражение (12.6) называют уравнением колебаний. Здесь А и a – постоянные зависящие от начальных условий; А называют амплитудой колебаний, a - начальной фазой, - фазой колебаний; - циклическая частота колебаний, т.е. число колебаний за 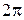секунд.

Часто для характеристики колебаний указывают период колебаний – Т (время одного полного колебания) и частоту колебанийn (число колебаний за единицу времени). Очевидно что,

(12.7)

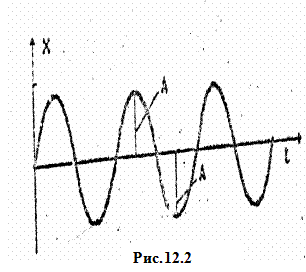
Выражение (12.6) показывает, что при данных условиях колебания являются гармоническими и незатухающими (рис.12.2).

Как уже отмечалось, строго незатухающих свободных колебаний не бывает. Дело в том, что энергия колеблющейся системы постепенно расходуется на преодоление сил трения, которые всегда имеют место, поэтому амплитуда колебаний уменьшается. Говорят, что колебания носят затухающий характер.

При небольших скоростях движения тела сила трения пропорциональна v:

. (12.8)

Уравнение движения маятника с учетом сил трения запишется так:

,

Или, вводя обозначения и перенося все слагаемые влево от знака равенства, получим

. (12.9)

Решением уравнения (12.9) является выражение

, (12.10)

где - циклическая частота свободных затухающих колебаний; - амплитуда колебаний. Она, очевидно, убывает с течением времени по экспоненте, A₀ - начальная амплитуда. График уравнения (12.10) представлен на рис.12.3. Величина характеризует скорость затухания. Она называется коэффициентом затухания.

Легко видеть, что , где t_e время колебаний, за которое амплитуда уменьшилась в е раз.

Скорость затухания характеризуют и двумя другими величинами: декрементом затухания , равным отношению двух соседних (отстоящих по времени на период Т) амплитуд. Логарифмическим декрементом затухания, равным, по определению, натуральному логарифму от декремента затухания:

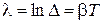. (12.11)

Оказывается, 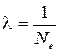, где N_е - число колебаний, за которое амплитуда уменьшается в е раз.