
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Работа 2. ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ растворов ПАВ
Цель работы:Определение поверхностного натяжения (s) растворов неионогенных ПАВ методом сталагмометра и установление зависимости s от концентрации раствора С.
Свободная поверхностная энергия единицы площади (т.е. избыток свободной энергии, приходящийся на 1см2 поверхностного слоя) s на границе жидкость — воздух обычно называется поверхностным натяжением, на границе жидкость — жидкость называется пограничным или межфазным натяжением (хотя эти термины, строго говоря, применимы для любой границы раздела).
Термин натяжение, возникший исторически, в связи с гипотезой упругой пленки, выражает представление о величине s как о силе, действующей тангенциально (т. е. в плоскости, касательной к поверхности). Таким образом, величину s можно определить равным образом как энергию и как силу, что легко показать, рассматривая изотермический процесс образования единицы новой поверхности.
Работа расширения поверхности, равная sdS, производится в плоскости, касательной к поверхности. Следовательно, всегда есть возможность рассматривать ее как работу против силы, действующей в этой плоскости в сторону сокращения поверхности. Если при таком расширении линия периметра, ограничивающего поверхность, длиной l, переместится на расстояние dx, то работа против силы fl равна fldx (где f — сила, приходящаяся на единицу длины). Из сравнения двух выражений для работы видно, что sdS = fldx, т. е. свободная энергия единицы поверхности (1 см2) численно равна тангенциальной силе, приходящейся на 1 см длины контура, ограничивающего поверхность раздела. Очевидно, что оба способа выражения должны быть эквивалентны в отношении размерности. Действительно, энергия единицы поверхности выражается в эрг/см2, т. е. в дин • см/см • см.
Сокращая, находим: дин/см или 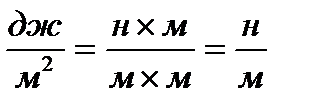 , т.е. размерность силы на единицу длины.
, т.е. размерность силы на единицу длины.
Таким образом, математически всегда возможна замена свободной энергии s величиной поверхностного натяжения, т. е. силы, действующей тангенциально к поверхности. Следует помнить, однако, что никаких особых сил, действующих только в поверхностном слое, мы не знаем. Работа увеличения поверхности совершается против тангенциальной составляющей тех же ван-дер-ваальсовых межмолекулярных сил, равнодействующая которых направлена нормально к поверхности в состоянии покоя.
При любом способе выражения величина s определяется работой, произведенной против сил молекулярного взаимодействия. Поэтому жидкости с более интенсивным полем молекулярных сил, т. е. более полярные, характеризуются высокими значениями s. Так, для сильно полярной жидкости — воды s = 72,75 эрг/см2 (72,75-10-3 дж/м2 или н/м) при 20°, для слабо полярного гексана s = 18,43 эрг/см2 (18,43 • 10-3 дж/м2) при той же температуре.
На границе двух жидкостей величина пограничного натяжения определяется разностью напряженностей силовых полей двух соприкасающихся фаз, и она всегда будет меньшей, чем наибольшее из поверхностных натяжений этих жидкостей на границе с воздухом.
Величина поверхностного натяжения уменьшается с ростом температуры (  < 0) вследствие ослабления сил молекулярного притяжения с увеличением среднего расстояния между молекулами.
< 0) вследствие ослабления сил молекулярного притяжения с увеличением среднего расстояния между молекулами.
Применение уравнения Гиббса — Гельмгольца к поверхности раздела
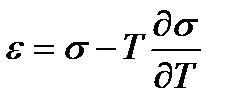 (2.1)
(2.1)
показывает, что полная поверхностная энергия единицы поверхности e больше ее свободной энергии s (так как  < 0) и слагается из двух величин s и T
< 0) и слагается из двух величин s и T  = q. Величина s равна максимальной работе процесса, в то время как q — (скрытая теплота образования поверхности) показывает, какое количество тепла поглощает система при изотермическом образовании 1см2 поверхности для поддержания постоянной температуры.
= q. Величина s равна максимальной работе процесса, в то время как q — (скрытая теплота образования поверхности) показывает, какое количество тепла поглощает система при изотермическом образовании 1см2 поверхности для поддержания постоянной температуры.
Причина поглощения тепла, с молекулярно-кинетической точки зрения, заключается в том, что молекулы движутся к поверхности, преодолевая молекулярное притяжение, направленное вглубь фазы; при этом скорость их уменьшается, и поверхность раздела образуется таким образом из молекул более «медленных», а следовательно, температура поверхностного слоя понижается, если энергия в форме тепла не подводится извне.
Уменьшение s с температурой происходит приблизительно линейно (  = const) до температур, близких к критической, где исчезает поверхность раздела фаз и s обращается в нуль. Дифференцирование уравнения (2.1) по Т, при условии
= const) до температур, близких к критической, где исчезает поверхность раздела фаз и s обращается в нуль. Дифференцирование уравнения (2.1) по Т, при условии  = const, приводит к выражению:
= const, приводит к выражению:
 =0; e≠f(T)
=0; e≠f(T)
Таким образом, полная поверхностная энергия единицы поверхности e является температурным инвариантом и может быть использована для сравнительной характеристики молекулярных сил в жидкостях различного состава и строения. Для определения e по формуле (2.1) необходимо измерить s и найти температурный коэффициент  , измеряя s при различных значениях Т.
, измеряя s при различных значениях Т.
Среди большого числа методов измерения поверхностного натяжения наиболее распространенными являются: 1) метод капиллярного поднятия, 2) метод наибольшего давления пузырьков, 3) метод отрыва кольца и 4) метод счета капель (метод сталагмометра).
Измерение поверхностного натяжения методом счета капель
 Метод сталагмометра является весьма распространенным, хотя и уступает в отношении точности другим методам измерения поверхностного натяжения. В основе метода лежит экспериментально установленное положение, что вес капли, медленно отрывающейся под действием силы тяжести от кончика вертикальной трубки, будет тем больше, чем больше поверхностное натяжение жидкости на границе с воздухом. В первом приближении можно считать, что сила поверхностного натяжения, действующая вертикально по окружности трубки и равная 2prs, поддерживает каплю, уравновешивая ее вес р. В момент отрыва р = 2prs.
Метод сталагмометра является весьма распространенным, хотя и уступает в отношении точности другим методам измерения поверхностного натяжения. В основе метода лежит экспериментально установленное положение, что вес капли, медленно отрывающейся под действием силы тяжести от кончика вертикальной трубки, будет тем больше, чем больше поверхностное натяжение жидкости на границе с воздухом. В первом приближении можно считать, что сила поверхностного натяжения, действующая вертикально по окружности трубки и равная 2prs, поддерживает каплю, уравновешивая ее вес р. В момент отрыва р = 2prs.
Это положение является справедливым в том случае, когда отрыв капли совершается по линии, равной внутреннему периметру капиллярной трубки радиуса r. В действительности же результаты киносъемки процесса падения капли показывают более сложную картину (Рис. 2.1), не позволяющую вывести строгую математическую зависимость между величинами р, s и r; в особенности трудно учесть ту часть капли, которая отрывается в виде маленькой капли или нескольких, следующих за основной.
В результате ряда экспериментальных работ была установлена зависимость:
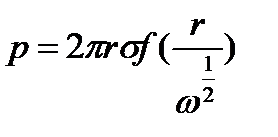
где f — функция от радиуса трубки r и объема капли w.
Обозначая 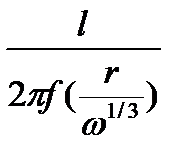 через F, получаем
через F, получаем
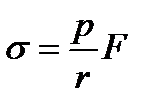
Для функции F в некоторых справочниках приведены таблицы, однако практически они применяются сравнительно редко ввиду трудностей определения радиуса капиллярной трубки. Обычно для измерения s пользуются стандартной жидкостью с известным поверхностным натяжением s0. В качестве стандартной применяют такую жидкость, которая образует капли, близкие по объему к каплям исследуемой жидкости, что позволяет исключить функцию F. Когда число капель двух жидкостей, вытекающих из одного и того же объема V сталагмометра, оказывается близким, значения функции F будут одинаковы, поскольку F мало изменяется с w (при изменении w в 1000 раз F изменяется от 0,17 до 0,26). Таким образом, для исследуемой жидкости s = (p/r)F, для стандартной s0=(p0/r)F0. При F = F0 из двух уравнений получим:
s/s0=p/p0
Отсюда:
s = s0(p/p0) (2.2)
Для водных растворов неорганических веществ в качестве стандартной жидкости применяют воду, так как в растворах поверхностно-инактивных веществ s изменяется приблизительно пропорционально концентрации и плотности, а следовательно, условие приближенного равенства объемов, может быть выполнено.
Для определения веса капли измеряют число капель n, вытекающих из объема V сталагмометра, а также плотность жидкости d, поскольку вес капли р может быть выражен формулой:
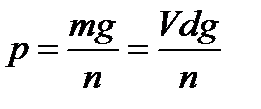 (2.3)
(2.3)
где m— масса жидкости в объеме V;
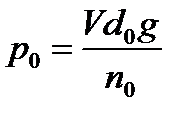 (2.4)
(2.4)
Подставляя (2.3) и (2.4) в (2.2), получим:
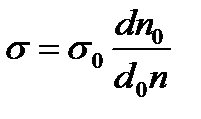 (2.5)
(2.5)
В другом способе вес капли р находят непосредственным взвешиванием отсчитанного целого числа капель.
В случае летучих жидкостей измерения проводят в стеклянной камере с насыщенным паром исследуемой жидкости.
Выполнение измерений
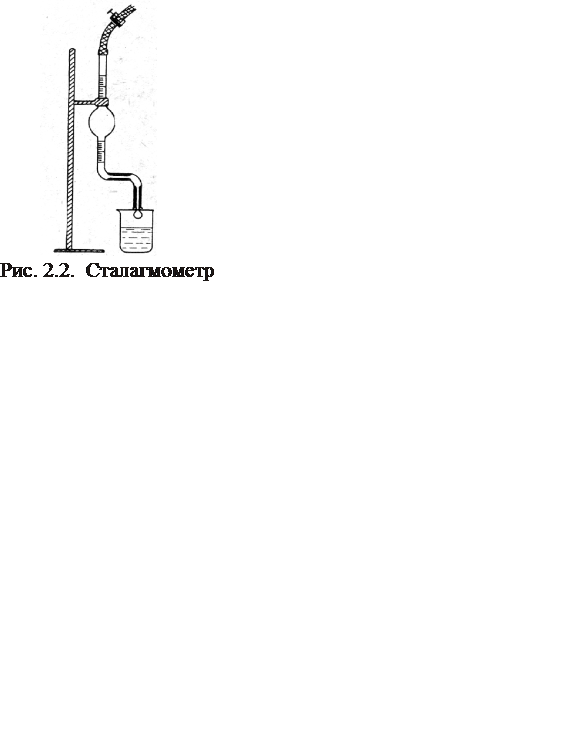
Сталагмометр представляет собой стеклянную трубку (часто коленчатую) с расширением в средней части и капилляром в нижней (рис. 2.2); на трубке нанесены две круговые метки (выше и ниже расширения). Целесообразно/ применять трубки, градуированные вблизи круговых .меток. Капилляр предназначен для ограничения скорости образования капель, которая не должна превышать 20 капель в 1 мин[1]; в зависимости от вязкости жидкости применяются капилляры различного диаметра. Внизу трубка оканчивается отшлифованной площадкой, в центре которой находится выходное отверстие капилляра. Перед началом работы сталагмометр промывают хромовой смесью, свободной от взвешенных частиц, затем тщательно промывают водой. Если кончик засорен, нельзя прочищать его иглой, проволокой и т. д., а надо промыть хромовой смесью или другой жидкостью. Необходимо содержать трубку и все части, соприкасающиеся с исследуемой жидкостью, в полной чистоте; совершенно недопустимо прикосновение пальцем или каким-либо предметом к нижней площадке после очистки.
Для измерения сталагмометр закрепляют в штатив, следя за тем, чтобы нижняя площадка находилась в горизонтальной плоскости (вытекающие капли должны иметь симметричную форму); надевая каучуковую трубку на верхний конец, засасывают жидкость выше верхней метки. Затем отсчитывают число капель, вытекающих из объема V от верхней до нижней круговой метки. Необходимо избегать сотрясений, толчков, колебаний воздуха и изменения температуры во время опыта.
Измерения производят вначале со стандартной жидкостью. Если таковой является вода, нет необходимости сушить сталагмометр после промывки, а также при переходе от воды к водным растворам. Во всех случаях необходимо перед измерением промыть сталагмометр исследуемым раствором. При измерении серии растворов различной концентрации, вначале следует измерять разбавленные растворы, переходя затем к более концентрированным. Плотность исследуемой жидкости d определяют при помощи пикнометра. Значения d0 и sо берут из таблиц для данной температуры. Для воды при 20оС sо = 72,75 эрг/см2; (72,75*10-3 н/м), d0 = 0,998 г/см3 (998 кг/м3). Вычисление ведут по формуле (2.5).
Целое число капель стандартной жидкости, ближе всего отвечающее объему V, заключенному между метками, собирают в бюкс, предварительно высушенный и взвешенный вместе с крышкой. Закрыв бюкс пришлифованной крышкой, взвешивают его вместе с жидкостью. Не выливая жидкости, повторяют опыт несколько раз, собирая капли в тот же бюкс и взвешивая. Определяют среднее значение веса Р0, деленного на число капель nо, т. е. p0 = P0/n0.
Таким же образом производят определение для исследуемой жидкости и вычисляют s по формуле (2.2).
ПРАКТИЧЕСКАЯ ЧАСТЬ
Задание 1. Определение поверхностного натяжения водных растворов ПАВ сталагмометром.
В качестве объекта исследования предлагаются водные растворы алифатических спиртов – неионогенных ПАВ.
Взять 10 колб или стаканчиков на 50-100 мл, пронумеровать их. Отмерить в первую из них пипеткой 30 мл исходного раствора ПАВ (выдает преподаватель), а в остальные – по 10 мл дистиллированной воды. Затем пипеткой перенести 20 мл ПАВ из колбы 1 во вторую, перемешать, 20 мл полученного раствора перенести в колбу 3 и т.д. В колбах получается раствор с последовательно убывающей концентрацией. Для каждого из растворов определить сталагмометром, как описано выше, поверхностное натяжение. При этом принять во внимание, что поверхностное натяжение воды сильно меняется с температурой. Полученные данные поместить в таблицу 2.1 и построить изотерму поверхностного натяжения в координатах s от С.
Таблица 2.1
Экспериментальные данные измерения сталагмометром
| Номер колбы | ||||||||||
| Концентрация ПАВ, моль/л | ||||||||||
| Число капель, шт. | ||||||||||
| Поверхностное натяжение, эрг/см2 |
СОДЕРЖАНИЕ И ОФОРМЛЕНИЕ ОТЧЕТА ПО РАБОТЕ
Отчет по работе содержит название, цели, краткое описание работы и выводы о поверхностной активности неионогенных ПАВ. Экспериментальные данные оформляются графически и заносятся в табл. 2.1. Графики подписываются исполнителями и прилагаются к работе.
Контрольные вопросы по работе 2.
1. Опишите механизм формирования адсорбционного слоя; объясните влияние адсорбционного слоя на поверхностное натяжение. Что такое поверхностная активность адсорбата?
2. В чем заключается метод определения s с помощью сталагмометра? Какие условия надо соблюдать при измерениях и почему?
Дата добавления: 2015-04-16; просмотров: 339; Мы поможем в написании вашей работы!; Нарушение авторских прав |