КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Применение обратных связей для управления электродвигателями
К современным электроприводам предъявляют высокие технические требования по точности, быстродействию, стабильности статических и динамических характеристик. Удовлетворить эти требования возможно лишь при применении обратных связей в электроприводах по углу, ускорению, моменту и.т.я
Электропривод с обратными связями в общем случае состоит из следующих узлов
рис. 1.1.
1. Системы автоматического управления, которая вырабатывает сигнал рассогласования между задающим сигналом и сигналом обратной связи, корректирует и фильтрует сигналы управления для необходимых статических и динамических характеристик.
2. Преобразования электрической энергии сети, преобразует электрическую энергию тока, напряжения, частоты сети для управления кабиной электродвигателя.
3. Преобразователь электрической энергии в механическую, представляющий собой электродвигатель постоянного тока.
4. Исполнительная механическая часть редуктора, передачи винт-гайка, объекты управления.
5. Измерительная часть с обратными связями, обеспечивающая измерение и обработку параметров объекта управления и передачи этой информации по каналам обратной связи в систему автоматического управления.
Задающий сигнал Сеть
Рис. 1.1.Функциоеальная схема электропривода
Влияние обратной связи по скорости на статические и динамические . характеристики электропривода.
Рассмотрим электропривод с отрицательной связью по скорости рис. 1.2. и сравним статические и динамические характеристики с обратной связью и без нее. Упращенная система уравнений, описывающая работу электродвигателя имеет вид:
(1.1) 
Решая эту систему уравнений с учетом и без учета обратной связи по скорости Uосс получим:
Без обратной связи: С обратной связью:
(1.2) 
(1.3)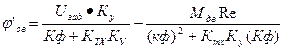 
из 1.3. видно, что при увеличении КТХ, КУ, в электроприводе с обратной связью колебания скорости вращения двигателя в зависимости от нагрузки уменьшается рис. 1.3., увеличивается жесткость механической характеристики.
Рис. 1.2. Структурная схема электропривода
(а) (б)
Рис. 1.3. Ступенчатое изменение
нагрузки от М1 до М2
Увеличение жесткости механической характеристики приводит к увеличению диапазона регулирования скорости.
Жесткость механической характеристики:
; (1.4)
Диапазон регулирования скорости:
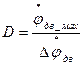; (1.5)
При анализе динамических характеристик электропривода опишем работу исполнительной механической части следующим уравнением:
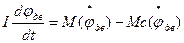; (1.6)
где I – момент инерции механизма;
Мс(f’дв) – момент сопротивления.
Для упрощения решения дифференциального уравнения будем считать, что Мс(f’дв) представляет собой линейную функцию скорости:
; (1.7)
Мс(f’дв)=0;
Подставим эти выражения в (1.6), получим:
; (1.8)
; (1.9)
где Тм=I/b – электромеханическая постоянная времени.
Решая дифференциальное уравнение (1.9) при начальных условиях получим уравнение переходного процесса скорости вращения электропривода:
; (1.10)
Из уравнения (1.9) видно, что увеличение жесткости b при наличии обратной связи по скоростям уменьшает электромеханическую постоянную времени Тм , существенно увеличивает быстродействие работы (рис.1.4), улучшая динамические характеристики электродвигателя.
Рис. 1.4. Переходной процесс в электроприводе.
5.2. Общий подход к синтезу электроприводов с обратной связью
Обычно синтез системы электропривода состоит из следующих этапов:
1.– формировка и обоснование требований, которым должна удовлетворять система;
2.– выбор функциональной схемы системы;
3.– выбор типа и расчет основных элементов регулятора;
- определение динамических свойств элементов системы;
4. – синтез корректирующего устройства регулятора;
5. – определение динамических свойств скорректированной
системы.
Формулировка требований к системе электропривода является весьма ответственны этапом ее синтеза. Требования составляют так, чтобы регулятор обеспечивал необходимые свойства объекта, был выполнен и мог быть рассчитан.
При выборе типа и расчете основных элементов регулятора исходят из того, чтобы регулятор мог осуществлять необходимые воздействия на электропривод. Кроме того должны быть обеспечены необходимая надежность, допустимые размер и вес, минимальная стоимость. В зависимости от назначения электропривода перечисленных общих требований.
Регуляторы – это один из наиболее важных функциональных элементов электропривода. Он обеспечивает необходимые динамические свойства электропривода – устойчивость и хорошее качество переходных процессов. От правильности выбора и выполнения регуляторов зависят, в большинстве случаев, работоспособность и качество всей системы. Поэтому выбор места включения, тока, схемы и параметров регуляторов является одним из основных этапов синтеза электропривода. Синтез даже наиболее простых систем электропривода не является строго определенной задачей. Это объясняется, прежде всего, многообразием требований, предъявляемых к системе: точность при медленно меняющихся воздействиях, качество переходной характеристики и т.д.
Динамические свойства элементов системы электропривода математически выражаются передаточными функциями, которые определяются исходя из принципа действия и технических данных элементов или по экспериментально полеченным частотным характеристикам. Последний этап отдается предпочтение тому или иному из позволяет иметь более точные сведения о свойствах элементов и обеспечивает большую точность расчетов. Поэтому экспериментальное определение частотных характеристик целесообразно во всех случаях, когда имеются реальные основные элементы системы или хотябы часть из них.
Динамические свойства определяют устойчивость системы электропривода. В большинстве случаев оказывается, что электропривод с первоначальными параметрами по своим динамическим свойствам не удовлетворяют требованиям: оказываются неустойчивой или имеет слишком малый запас устойчивости и плохие показатели качества.
Улучшение динамических свойств системы может быть достигнуто при правильно сконструированном регуляторе.
5.3. Основные схемы регуляторов
Рассмотрим основные схемы регуляторов, которые используются в системах управления электроприводами.
Пропорциональный регулятор (П - регулятор) (рис.1.5.)
В простейшем случае, когда усилитель безинерционный и корректирующее устройство отсутствует, то такой регулятор называется пропорциональным. Сопротивления Z0 и Z1 являются омическими сопротивлениями. Передаточная функция регулятора имеет вид:
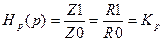(1.11)
рис. 1.5.П-регулятор.
Интегральный регулятор (И - регулятор) рис.1.6.
Заменив в цепи обратной связи резистор R1 конденсатором С1, получим интегральный регулятор.
; 
;
; (1.12)
где Т1 – постоянная интегрирования.
Рис. 1.6. И-регулятор.
Пропорционально – интегральный регулятор (ПИ - регулятор) рис.1.7.
Если в цепи обратной связи оставить и резистор R1, и конденсатор С1, то переходная характеристика системы должна быть суммарной из двух вышестоящих характеристик.
; 
;
(1.13)
передаточную функцию регулятора можно записать ив другом виде:
, (1.14)
где 
- постоянная времени изодрома.
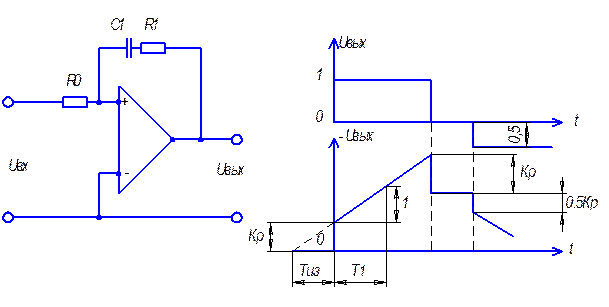
Рис. 1.7. ПИ-регулятор.
Пропорционально – дифференциальный регулятор (ПД - регулятор)
рис.1.8
объединяет в себе свойства пропорционального и дифференциального регуляторов; в стационарном режиме работает как пропорциональный усилитель входного сигнала, но при изменении напряжения на входе регулятора к его выходному напряжению добавляют напряжение соответствующее скорости изменения входного сигнала (чем больше изменение, тем больше выходное напряжение). Передаточная функция регулятора рассчитывается по формуле:
(1.15)
Рис. 1.8. ПД-регулятор
При скачкообразном изменении входного сигнала площадь графика переходного процесса выходного напряжения определяется формулой:
(1.16)
Площадь fD ограничена линией асе.
Пропорционально – интегрально – дифференциальный регулятор (ПИД – регулятор) рис. 1.9
Изложенные выше сведениям о ПИ и ПД – регуляторах позволяют сконструировать цепь обратной связи так, чтобы получить регулирование по ПИД закону. Передаточная функция ПИД регулятора имеет вид:
(1.17)
Вводя сокращения Т1=R0C1 – постоянная интегрирования;
(1.18)
Рис. 1.9. ПИД –регулятор
5.4. Синтез электроприводов с последовательными корректирующими устройствами, регуляторами
Если корректирующее устройство включено впрямую цепь системы последовательно с её основными элементами, то оно называется последовательным.
Рис. 1.10.Функциональнаясхема электропривода.
На рис.1.10 показана функциональная схема электропривода, в которой последовательное корректирующее устройство включено непосредственно сравнивающего элемента. Однако в большинстве случаев оно включается между каскадами усилителя и конструктивно совмещается с ним.
Сигнал рассогласования проходит через последовательное корректирующее устройство и соответствующим образом преобразуется им. Таким образом обеспечивается необходимый закон регулирования, т.е. вид дифференциального уравнения, определяющего зависимость управляющего согнала от несогласования.
Для получения необходимых динамических и статических характеристик электропривода строится желаемая логарифмическая амплитудночастотная характеристика Ж ЛАЧХ.
При синтезе корректирующих устройств в электроприводах в качестве типового, т.е. наиболее характерного внешнего воздействия, принято считать ступенчатое изменение задающего воздействия. Указанный режим наиболее тяжелой, и поэтому предполагается, что если система имеет хорошие показатели качества переходного процесса при ступенчатом задающем воздействии, то оно будет высококачественной при других видах задающего воздействия.
В простейшем случае синтез регулятора можно производить исходя из обеспечения заданного значения передаточного коэффициента К разомкнутой цепи системы и следующих показателей качества:
Порядок астатизма
Времени регулирования
Максимального перерегулировеия
Кроме того, очень часто должны быть обеспечены необходимые знания коэффициентов ошибки оп скорости и ускорению.
Построение Ж ЛАЧХ целесообразно производить в следующем порядке:
- строится асимптотическая ЛАЧХ неизменяемой части системы электропривода.
Эту часть системы составляют те её элементы, необходимость которых установлена при выборе функциональной схемы.В неизменяемую
входят все элементы функциональной схемы. Параметры элементов неизменяемой части частично заданы (или определены экспериментально). Характеристика строится для разомкнутого состояния системы, примерный вид её на (рис.1.11).
Рис.1.11. ЛАЧХ.
- строится низкочастотная асимптота Ж ЛАЧХ.
Наклон низкочастотной Ж ЛАЧХ должен быть равен -20 
дб/дек. При частоте w=1 ордината этой асимптотыили её продолжениядолжна быть равна 20LgK.
- определяется частота среза wc.
; (1.19)
где tp – время переходного процесса.
- строится среднечастотная асимптота Ж ЛАЧХ. Она проводится через точку wc на оси абсцисс с наклоном - 20 бб/дек . Такой наклон выбирается потому, что меньший наклон трудно осуществим, а больший не обеспечивает необходимого запаса устойчивости.
- Определяется необходимый запас устойчивости.
- Среднечастотная асимптота сопрягается с низкочастотной . Сопрягающая асимптоты строится так, чтобы частота w1 была возможно большей, наклон асимптоты возможно меньше отличается от наклона ЛАЧХ неизменяемой части системы на данном участке частоты, а избыток фазы
, при частоте wа был не меньше 
. - Среднечастотная асимптота сопрягается с высокочастотной наиболее целесообразно, чтобы высокочастотная асимптота Ж ЛАЧХ совпадает с высокочастотной асимптотой ЛАЧХ неизменяемой части системы.
Комплексный передаточный коэффициент разомкнутой системы и её ЛАЧХ определяются в этом случае следующими выражениями:
(1.19)
(1.20)
где WH (iw) и AiH(w) – комплексный передаточный коэффициент и Н ЛАЧХ;
Wпос(jw) и Aiпос(w) – тоже последовательного передаточного устройства.
Требования, предъявляемые к системе, будут удовлетворены, если ЛАЧХ разомкнутой цепи скорректированной системы будут совпадать с ЖЛАЧХ.
(1.21)
(1.22)
На рисунке получена ЛАЧХ последовательного корректирующего устройства.
Дата добавления: 2015-04-16; просмотров: 199; Мы поможем в написании вашей работы!; Нарушение авторских прав |