
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Синтез электроприводов с параллельными корректирующими устройствами, регуляторами
Последовательное корректирующее устройство имеет недостатки, которые состоят в следующем: если сигнал содержит помехи, то при дифференцировании с применением ПД, ПИД регуляторов уровень помех может значительно повысится, поэтому применение в отдельных случаях последовательного корректирующего устройства может быть применимым.
Параллельное корректирующее устройство называется параллельным, если оно включено встречно – параллельно одному из участков прямой цепи передачи сигнала в системе электропривода, т. е. осуществляет местную обратную связь.
Параллельное корректирующее устройство изменяет динамические свойства того участка прямой цепи системы, который она охватывает обратной связью, и таким образом обеспечивает необходимое изменение динамических свойств всей системы электропривода. Это влияние не систему определяется тем, что передаточная функция соединения из участка прямой цепи с передаточной функцией Wохв(S) и параллельного корректирующего устройства с передаточной функцией Wпар(S), осуществляющего отрицательную обратную связь, имеет следующий вид.
 ; (1.23)
; (1.23)
чрезвычайно важно, что если в определенном интервале частот соблюдается условие 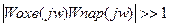 , то в этом интервале частот
, то в этом интервале частот
 (1.25)
(1.25)
Следовательно при выполнении условия (1) преобразование сигнала на участке с параллельным корректирующем устройством определяются только свойства самого корректирующего устройства. Условие (1) выполняется достаточно легко и в широком диапазоне частот, когда в рассматриваемый контур входит усилитель или его часть и передаточной коэффициент разомкнутой цепи контура КохвКпар>>1. таким образом, с помощью параллельного корректирующего устройства можно устранить (или существенно уменьшить) нежелательное влияние какого – либо элемента системы на её динамические свойства и одновременно обеспечить необходимое преобразование сигнала на этом участке и придать системе желаемые динамические свойства.
Параллельное корректирующее устройство так же, как и последовательное, позволяет удовлетворить разнообразные требования и широко применяться в системах электроприводов. Более того, по сравнению с последовательным, оно имеет существенные преимущества:
Параллельное корректирующее устройство устраняет (или значительно уменьшает) влияние нестабильности параметров, охваченных им элементов на динамические свойства системы;
Сигнал создаваемый параллельным корректирующим устройством, не нуждается в усилении;
Меньше вероятность повышения уровня помех при дифференцировании сигнала;
5.6. Синтез электроприводов с последовательными и параллельными корректирующими устройствами, регуляторами]
Стремление скорректировать динамические свойства системы электропривода с помощью одного последовательного или параллельного корректирующего устройства может привести к необходимости иметь слишком сложное или даже технически неосуществимое корректирующее устройство. Поэтому очень часто в системе предусматривают два корректирующих устройства – последовательное и параллельное.
При синтезе строится сначала ЛАЧХ неизменяемой части электропривода Wн(jw) и желаемая ЛАЧХ Wж(jw). Вычитая Wн(jw) из Wж(jw), получаем ЛАЧХ Wk(jw) последовательного корректирующего устройства и участка цепи с параллельным корректирующим устройством.
ЛАЧХ Wk(jw) нужно разложить на две составляющие одинаковой, приблизительно, сложности, т. е. имеющих равное количество асимптот с равными наклонами. Одна из составляющих будет ЛАЧХ последовательного корректирующего устройства Wж(jw). другая составляющая будет ЛАЧХ участка цепи с параллельным корректирующим устройством Wж(jw). Если выполняется условие (1-16), то ЛАЧХ параллельного корректирующего устройства Wпр(jw)= Wkн(jw).
Рассмотрим несколько вариантов разложение суммарной ЛАЧХ Wk(jw) на составляющие и выбрать из них тот, при котором корректирующие устройства наиболее легко выполнимы.
На рис.1.13 в виде примера определена суммарная ЛАЧХ Wk(jw) и дано два варианта разложения её на составляющие. По первому варианту (а) оба корректирующих устройства должны быть интегрирующими, по второму (б) – дифференцирующими.
После определения ЛАЧХ требуемых корректирующих устройств необходимо составить их корректирующие функции, выбрать тип и определить параметры элементов, а затем построить переходную характеристику и проверить, соответствуют ли полученные показатели качества заданным требованиям.
Если электропривод содержит ряд параллельных цепей обратной связи, охватывающих одну и туже последовательность звеньев, то удобно использовать обратные логарифмические частотные характеристики, которые обеспечивают большую простоту и наглядность расчетов многоконтурных систем.

Рис.1.12. Структурная сжема электропривода с последовательной и параллельной коррецией.

Рис1.13 ЛАЧХ.
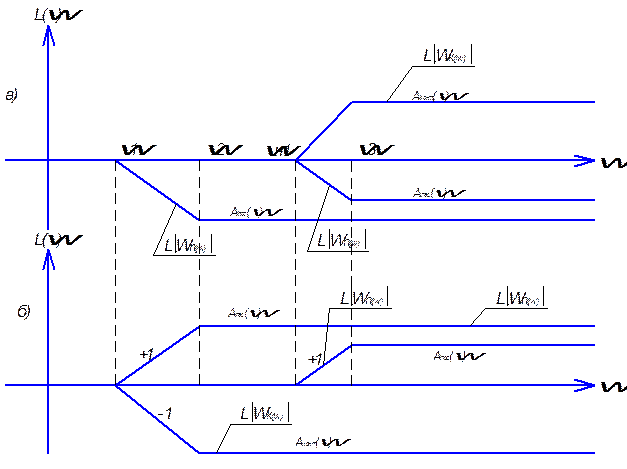
Рис.1.14. ЛАЧХ.
Метод с обратными ЛАЧХ основан на связи качества системы с ее частотными свойствами, а именно, с точностью воспроизведения гармонического воздействия на входе и с показаниями колебательности М. показателями качества системы служат ошибка при движении с постоянной скоростью (скоростная ошибка  СК), ошибка при движении по гармоническому закону (динамическая ошибка
СК), ошибка при движении по гармоническому закону (динамическая ошибка  Д), показатель колебательности М, определяющий запас устойчивости и склонность системы к колебаниям.
Д), показатель колебательности М, определяющий запас устойчивости и склонность системы к колебаниям.
Таблица V.I.
| Тип ЛАХ | Передаточная функция W (s) | Наклон в интервале частот, дБ/дек | |||
| 0 – w1 | w1 – w2 | w2 – w3 | w3 - 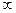 
| ||
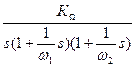
| -20 | -40 | -40 | -40 | |
| I | 
| -20 | -40 | -20 | -40 |
| II | 
| -20 | -60 | -20 | -40 |
| III | 
| -20 | -40 | -20 | -60 |
| IV | 
| -20 | -60 | -20 | -60 |
Типовые ЛАХ представлены на рис.1.15, (ЛАХ-0,ЛАХI—ЛАХIV). Передаточные функции и ЛАХ полностью определяются заданием четырех величин: коэффициента усиления (добротности) Кw и трех сопрягающих частот w1 = 1/T1; w2 = 1/T2; w3 = 1/T3.
Известна следующая характеристика рассматриваемых типов ЛАХ. Для того чтобы показать зависимость максимально допустимой добротности системы Кw по условиям запаса устойчивости от типа ЛАХ при одной и той же частоте среза, на рис. V.1 построены все типовые ЛАХ для wc = 10 1/с.
ЛАХ-1—ЛАХ-IV имеют одинаковые значения сопрягающих частот w1, w2, w3 и протяженность среднечастотного участка h = w3/w2.
Для облегчения построения желаемой ЛАХ вводят типовые передаточные функции и соответствующие им ЛАХ. Передаточные функции и ЛАХ-I—ЛАХ-IV имеют одинаковые значения сопрягающих частот w1,w2,w3, и протяженность среднечастотного участка h = w3/w2.
По условиям запаса устойчивости следящие системы с ЛАХ-0 могут иметь первую сопрягающую частоту не ниже частоты среза, т. е. w1>wc. Увеличение добротности следящей системы связано с необходимостью повышения wc, а следовательно, и ее граничной частоты wгр. Для увеличения добротности необходимо повышение сох (уменьшение первой постоянной времени Т1). Применение характеристик типа ЛАХ-0 целесообразно для получения быстродействующих следящих систем без корректирующих цепей и следящих систем, стабилизированных отрицательным наклоном механической характеристики исполнительного двигателя (вязким трением), отрицательной обратной связью по скорости, дифференцирующей корректирующей цепью и пропорциональной составляющей, включенной последовательно.
ЛАХ-I и ЛАХ-Ш — наиболее распространенная форма логарифмических характеристик, свойственная следящим системам с сравнительно большой добротностью при относительно низкой частоте среза wc. Как видно из рис. 1.15, ЛАХ-I и ЛАХ-Ш отличаются только в их высокочастотной части.
Типовые ЛАХ-I—ЛАХ-IV для систем с астатизмом второго порядка отличаются тем, что в низкочастотной области имеют асимптоту только с наклоном — 40 дБ/дек. Запас устойчивости для ЛАХ систем с астатизмом первого и второго порядков определяется протяженностью среднечастотного участка ЛАХ  , который выбирают или в зависимости от заданного коэффициента колебательности М, или по методике В. В. Солодовникова с использованием номограмм, определяющих участки +L1 и —Lx. Добротность для ЛАХ-I и ЛАХ-Ш определяют из соотношения
, который выбирают или в зависимости от заданного коэффициента колебательности М, или по методике В. В. Солодовникова с использованием номограмм, определяющих участки +L1 и —Lx. Добротность для ЛАХ-I и ЛАХ-Ш определяют из соотношения  . Она в w2/w1 раз больше, чем в следящих системах c ЛАХ – 0, а частота среза wc соответственно при равных добротностях может быть в w1/w2 раз ниже:
. Она в w2/w1 раз больше, чем в следящих системах c ЛАХ – 0, а частота среза wc соответственно при равных добротностях может быть в w1/w2 раз ниже: 
 РиРис.1.15
РиРис.1.15
Типовые логарифмические амплитудно – частотные характеристики.
Поскольку граничная частота wгр замкнутой системы определяется wc разомкнутой системы (wгр = 1,5 - 2 wc), то в случае ЛАХ-1 и ЛАХ-Ш система может иметь относительно высокую добротность при низкой wгр.
ЛАХ-1 и ЛАХ-Ш отличаются тем, что при них увеличение добротности не связано с необходимостью изменения wc. При фиксированных значениях wc, w2, w3 и h увеличение добротности вызывает необходимость понижения w1 Поскольку в рационально спроектированной системе первая сопрягающая частота w1 не должна быть ниже максимальной частоты изменения входного сигнала, при ЛАХ-1 и ЛАХ-Ш увеличение добротности может вызвать необходимость некоторого повышения частоты среза, но значительно меньшего, чем при ЛАХ-0.
ЛАХ-П и ЛАХ-IV отличаются от ЛАХ-1 и ЛАХ-Ш наклоном, равным 60 дБ/дек, в интервале частоты w1 - w2. Здесь добротность определяют из соотношения:
 , (1.26)
, (1.26)
и она может быть значительно больше, чем при ЛАХ-1 и ЛАХ-Ш при тех же wc и интервале w1 - w2. Соответственно при равных добротностях в следящих системах с ЛАХ-П и ЛАХ-IV wc будет ниже.
ЛАХ-1 и ЛАХ-Ш, а также ЛАХ-П и ЛАХ-IV имеют следящие системы, стабилизированные отрицательной обратной связью по ускорению; интегро-дифференцирующей корректирующей цепью, включенной последовательно.
ЛАХ-1 и ЛАХ-Ш и особенно ЛАХ-П—ЛАХ-IV целесообразно применять, когда необходима высокая точность слежения при относительно низкой граничной частоте пропускания системы.
Следящие системы с ЛАХ-П, ЛАХ-IV могут иметь АФХ, при которой они относятся к условно устойчивым системам. В таких системах в случае согласования с «большого угла», выходящего за пределы линейного участка характеристики, например в режиме синхронизации при первичном включении системы, могут возникать медленно затухающие или даже незатухающие колебания. Поэтому условно устойчивые системы, как правило, не применяются.
В работе [2] составлены таблицы, в которых дана зависимость показателя колебательности замкнутой системы М от протяженности h среднечастотного участка желаемой ЛАХ и других ее параметров для следящих систем с астатизмом первого и второго порядков.
При синтезе корректирующих устройств за исходную передаточную функцию системы принимают передаточную функцию  . Для приведенной выше структурной схемы (см. рис. 9).
. Для приведенной выше структурной схемы (см. рис. 9).
 (1.27)
(1.27)
Число слагаемых, составляющих обратную передаточную функцию разомкнутой СС, равно числу замкнутых внутренних контуров, включая главную обратную связь.

Рис.1.16 Синтез с использованием ЛАЧХ
Если ПКУ в систему не введено, то вместо равенства (1.16 получаем Wp-1 (s) = Wн.ч.-1(s) + Z (s). Таким образом, обратная передаточная функция равна сумме двух слагаемых, первое из которых представляет собой обратную передаточную функцию разомкнутой следящей системы без местной обратной связи, а второе характеризует цепь местной обратной связи.
Упрощение, достигаемое при анализе и синтезе следящих систем с использованием обратных ЛАХ, связано с указанной возможностью представления функции Wp-1 (s). В самом деле, из последнего равенства видно, что в диапазоне частот, для которых  , приближенно имеем
, приближенно имеем 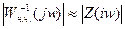 ; в диапазоне частот, для которых
; в диапазоне частот, для которых  , приближенно получим
, приближенно получим  . Следовательно,
. Следовательно,  может быть приближенно определена в результате простого визуального сопоставления ЛАХ
может быть приближенно определена в результате простого визуального сопоставления ЛАХ  и
и  , (точнее, в результате их векторного сложения).
, (точнее, в результате их векторного сложения).
На рис. V.4 изображены ЛАХ, соответствующие функциям  и
и  . Из рисунка видно, что в диапазоне частот w<wа и w<wб справедливо неравенство
. Из рисунка видно, что в диапазоне частот w<wа и w<wб справедливо неравенство  >
>  , а в диапазоне частот wа<w<wб неравенство
, а в диапазоне частот wа<w<wб неравенство  <
<  . Следовательно в диапазоне частот w<wа и w<wб асимптоты обратной ЛАХ разомкнутой системы
. Следовательно в диапазоне частот w<wа и w<wб асимптоты обратной ЛАХ разомкнутой системы 

 В диапазоне частот wа<w<wб
В диапазоне частот wа<w<wб 

 . Поэтому обратная ЛАХ разомкнутой системы
. Поэтому обратная ЛАХ разомкнутой системы  приближенно может быть представлена в виде ломаной ABCDEF. Здесь обратную ЛАХ
приближенно может быть представлена в виде ломаной ABCDEF. Здесь обратную ЛАХ  на каждом участке приближенно определяют непосредственно из рисунка и принимают совпадающей с той из двух характеристик
на каждом участке приближенно определяют непосредственно из рисунка и принимают совпадающей с той из двух характеристик  и
и  , которая является большей по своей ординате. При этом легко проследить изменение характеристики
, которая является большей по своей ординате. При этом легко проследить изменение характеристики  при изменении характеристики цепи обратной связи
при изменении характеристики цепи обратной связи  , что имеет важное значение при синтезе системы.
, что имеет важное значение при синтезе системы.
Следовательно, построение обратной ЛАХ  осуществляется более просто и наглядно, чем построение ЛАХ
осуществляется более просто и наглядно, чем построение ЛАХ  . Эти преимущества особенно проявляются при синтезе многоконтурных СС.
. Эти преимущества особенно проявляются при синтезе многоконтурных СС.
Исследование следящих систем с помощью обратных ЛАХ обычно проводят на миллиметровой бумаге, при этом наиболее удобен масштаб по оси частот 1 декада —50 мм, а по оси децибел 1 декада (20 дБ) — 25 мм.
Сущность методики синтеза следящих системы с использованием обратных ЛАХ сводится к следующему. Выбираем желаемую обратную логарифмическую амплитудно-частотную характеристику  разомкнутой системы (сплошная линия на рис. 1.16) по известной методике [15]. Дальнейшая задача состоит в определении передаточных функций Z (s) и kП0 (s), при которых справедливы приближенные равенства
разомкнутой системы (сплошная линия на рис. 1.16) по известной методике [15]. Дальнейшая задача состоит в определении передаточных функций Z (s) и kП0 (s), при которых справедливы приближенные равенства 



 , что имеет место, если
, что имеет место, если


 (1.28)
(1.28)
Строим ЛАХ, соответствующую первому слагаемому правой части равенства (1.28), т. е. логарифмическую характеристику  (штриховая линия на рис. 1.16) так, чтобы ее низкочастотная и высокочастотная части совпали с характеристикой
(штриховая линия на рис. 1.16) так, чтобы ее низкочастотная и высокочастотная части совпали с характеристикой  . Передаточную функцию kП0 (s) последовательного корректирующего устройства выбираем из соображений, рассмотренных выше. При выборе передаточной функции параллельного корректирующего устройства необходимо обеспечить, чтобы ЛАХ
. Передаточную функцию kП0 (s) последовательного корректирующего устройства выбираем из соображений, рассмотренных выше. При выборе передаточной функции параллельного корректирующего устройства необходимо обеспечить, чтобы ЛАХ  , соответствующая второму слагаемому правой части (1.16), в диапазоне средних частот wа<w<wб совпала с
, соответствующая второму слагаемому правой части (1.16), в диапазоне средних частот wа<w<wб совпала с  . Для этого продолжим асимптоты желаемой характеристики, соответствующие второй низкочастотной асимптоте и первой среднечастотной асимптоте (иногда вторая среднечастотная асимптота), неограниченно влево и вправо и примем полученную таким образом ЛАХ за характеристику
. Для этого продолжим асимптоты желаемой характеристики, соответствующие второй низкочастотной асимптоте и первой среднечастотной асимптоте (иногда вторая среднечастотная асимптота), неограниченно влево и вправо и примем полученную таким образом ЛАХ за характеристику  . При этом, как видно из рис.1.16, удовлетворяется равенство (1.16). Действительно, для w<wа и w>wб
. При этом, как видно из рис.1.16, удовлетворяется равенство (1.16). Действительно, для w<wа и w>wб  <
<  и для интервалов частот w<wа и w>wб
и для интервалов частот w<wа и w>wб 

 . С другой стороны, в интервале средних частот wа<w<wб
. С другой стороны, в интервале средних частот wа<w<wб  >
>  , и поэтому для указанного интервала частот wа<w<wб
, и поэтому для указанного интервала частот wа<w<wб


 (1.29)
(1.29)
Аналитическое выражение второго слагаемого правой части равенства ( ) для случая, представленного на рис., имеет вид:
 (1.30)
(1.30)
Следовательно, искомая передаточная функция:
 (1.31)
(1.31)
Необходимо убедиться, что внутренний контур местной обратной связи системы устойчив. Для определения запаса устойчивости внутреннего контура по фазе следует найти разность фаз:

при значениях частот w=wа и w=wб, соответствующих точкам пересечения В и D (рис1.16) двух логарифмических характеристик:
 и
и  .
.
Запас устойчивости внутреннего контура по фазе определяется равенством:
 . (1.31)
. (1.31)
Величина µ определяется при значении частоты w=wб. Нетрудно убедиться в справедливости формулы (V.3). Действительно, передаточная функция разомкнутого внутреннего контура обратной связи:
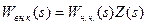 .
.
Контур находится на границе устойчивости, если при некотором значении частоты со справедливо равенство Wн.ч.(jw)Z(jw)=-1, которое может быть заменено системой равенств:
 (1.32)
(1.32)
В точках пересечения двух характеристик  и
и  , т. е. при w=wа и w=wб, удовлетворяется первое равенство системы (V.4).
, т. е. при w=wа и w=wб, удовлетворяется первое равенство системы (V.4).
Если при этом величина имеет положительное значение, то внутренний контур имеет запас устойчивости по фазе.
На практике обычно бывает достаточно проверить значение запаса устойчивости по фазе в точке D, так как в точке В запас устойчивости по фазе имеет, как правило, достаточное значение. При необходимости значение запаса устойчивости по фазе в точке В следует вычислять по формуле:
 (1.33)
(1.33)
Запас устойчивости внутреннего контура по амплитуде можно определить и графическим способом, если построить ЛАХ  разомкнутого внутреннего контура. Для этого из характеристики
разомкнутого внутреннего контура. Для этого из характеристики  необходимо графически вычесть характеристику
необходимо графически вычесть характеристику  (рис. 1.17). Если запас устойчивости внутреннего контура окажется недостаточным, то справа или слева от точки D (см. рис. V.4) следует изменить наклон асимптоты
(рис. 1.17). Если запас устойчивости внутреннего контура окажется недостаточным, то справа или слева от точки D (см. рис. V.4) следует изменить наклон асимптоты
характеристики  , таким образом, чтобы запас устойчивости имел требуемое значение. Естественно, что при этом изменится вид передаточной функции Z (s).
, таким образом, чтобы запас устойчивости имел требуемое значение. Естественно, что при этом изменится вид передаточной функции Z (s).
Для определения µ, нет необходимости строить логарифмические фазочастотные характеристики отдельных звеньев. Значения аргументов удобно определять с помощью шаблонов [2], масштаб которых по оси частот совпадает с масштабом, рекомендованным выше. С помощью шаблонов можно найти запас устойчивости по фазе системы в целом. Для этого достаточно вычислить разность:
 (1.34)
(1.34)
где wc частота среза системы. Шаблон удобно применять и для построения обратной логарифмической фазочастотной характеристики argWp-1(jw) разомкнутой системы; эту характеристику затем можно использовать для определения запаса устойчивости системы по амплитуде.
Для точного построения логарифмических частотных характеристик разомкнутой и замкнутой систем (  и
и  =
=  ) целесообразно использовать графическое сложение векторов соответствующих слагаемых.
) целесообразно использовать графическое сложение векторов соответствующих слагаемых.

Рис.1.17. Структурная схема электропривода с паралельными и последовательными корректирующими устройствами.
Известные методики позволяют определить как последовательные, так и параллельные корректирующие устройства [2]. В общем случае структурную схему следящей системы можно представить в виде схемы на рис. 1.17. Передаточная функция разомкнутой системы имеет вид:
 ; (1.35)
; (1.35)
где Wн.ч. (s) — передаточная функция силового агрегата со схемой управления, выбранного при энергетическом расчете; kП0 (s) — передаточная функция предварительных каскадов усиления с последовательным корректирующим устройством; Z (s) — передаточная функция обратных стабилизирующих (корректирующих) связей, например отрицательная обратная связь по скорости или ускорению выходного вала.
При синтезе корректирующих устройств и связей необходимо так выбрать передаточные функции kП0 (s) и Z (s), чтобы общая передаточная функция разомкнутой системы Wp (s) приближалась к передаточной функции, описывающей желаемую характеристику системы.
Предположим, что в соответствии с требованиями к качественным показателям системы автоматического регулирования выбрана желаемая логарифмическая частотная характеристика  разомкнутой системы (вид и положение асимптот, сопрягающие частоты w1 ,w2 ,w3 ). Пусть передаточная функция неизменяемой части системы имеет вид:
разомкнутой системы (вид и положение асимптот, сопрягающие частоты w1 ,w2 ,w3 ). Пусть передаточная функция неизменяемой части системы имеет вид:
 (1.36)
(1.36)
Строим ЛАХ неизменяемой части системы при коэффициенте усиления  :
:
 (1.37)
(1.37)
Для выполнения заданных требований по точности низкочастотная асимптота характеристики неизменяемой части системы должна совпадать с низкочастотной асимптотой желаемой ЛАХ или проходить выше ее (рис. V.3).

Рис.1.18 ЛАЧХ.
При этом высокочастотные асимптоты желаемой ЛАХ и ЛАХ неизменяемой части, как правило, не совпадают. Эти характеристики можно совместить, сдеформировав ЛАХ неизменяемой части введением последовательного корректирующего устройства (ПКУ). Если высокочастотная асимптота силового агрегата проходит ниже высокочастотной асимптоты желаемой ЛАХ, то вводят дифференцирующий контур, если выше, то интегрирующий.
На рис. 1.18 ЛАХ неизменяемой части проходит ниже желаемой ЛАХ, поэтому на частоте w2 введем дифференцирующее ПКУ с передаточной функций вида:
 (1.38)
(1.38)
Обычно выбирают k1 = 0,05 - 0,1, что приводит к ослаблению основного сигнала ошибки в 10—20 раз. Однако это ослабление компенсируется увеличением коэффициента усиления последующих усилительных устройств. Введением последовательного корректирующего устройства получаем характеристику  , которая совпадает с желаемой в области высоких и низких частот, но не совпадает с желаемой в области средних частот. За высокочастотные асимптоты желаемой ЛАХ принимают высокочастотные асимптоты ЛАХ неизменяемой части системы.
, которая совпадает с желаемой в области высоких и низких частот, но не совпадает с желаемой в области средних частот. За высокочастотные асимптоты желаемой ЛАХ принимают высокочастотные асимптоты ЛАХ неизменяемой части системы.
Среднечастотную часть характеристики разомкнутой системы можно сформировать с помощью параллельных корректирующих устройств. В области средних частот выражение, стоящее в знаменателе передаточной функции разомкнутой СС, существенно больше единицы. Тогда в этой области для разомкнутой СС приближенно можно принять:
 (1.39)
(1.39)
Таким образом, если корректирующая отрицательная обратная связь является глубокой для частот в районе wc, то ЛАХ Wp(jw) скорректированной системы целиком определяется ЛАХ корректирующей отрицательной обратной связи. Это справедливо, когда ЛАХ Wн.ч.(jw) в районе wc выше ЛАХ Wж(jw) не менее, чем на 20 дБ.
Если в качестве асимптот  принять асимптоты соответствующей части желаемой характеристики, то на всем диапазоне частот желаемая характеристика и ЛАХ разомкнутой СС будут совпадать (рис. V.3).
принять асимптоты соответствующей части желаемой характеристики, то на всем диапазоне частот желаемая характеристика и ЛАХ разомкнутой СС будут совпадать (рис. V.3).
Для определения устойчивости внутреннего контура СС находят ЛАХ внутреннего контура, которую определяют как разность:
 (1.40)
(1.40)
Соответствующие построения приведены на рис. 1.18. Получив ЛАХ внутреннего контура, анализируют его устойчивость.
Дата добавления: 2015-04-16; просмотров: 1509; Мы поможем в написании вашей работы!; Нарушение авторских прав |