
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основные теоретические сведения. Резонансомв электрической цепиили на участке, содержащем катушки индуктивности и конденсаторы, называется явление
Резонансомв электрической цепиили на участке, содержащем катушки индуктивности и конденсаторы, называется явление, при котором гармонические напряжение и ток на входе цепи совпадают по фазе. Цепь, состоящая из параллельно соединенных индуктивной и емкостной ветви, в которых наблюдается резонанс токов, называется параллельным колебательным контуром.
 а
а
|  б
б
|
| Рис. 6.1. Параллельный колебательный контур |
На рис. 6.1, а приведена схема параллельного колебательного контура. При резонансе реактивные составляющие токов в катушке индуктивности  и конденсаторе
и конденсаторе  компенсируют друг друга (рис. 6.1, б).
компенсируют друг друга (рис. 6.1, б).
В режиме резонанса ток  и напряжение
и напряжение  на входе контура совпадают по фазе. Определим токи в ветвях:
на входе контура совпадают по фазе. Определим токи в ветвях:
 (6.1)
(6.1)
 (6.2)
(6.2)

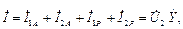 (6.3)
(6.3)
где  ,
,  и
и  – активные проводимости ветвей;
– активные проводимости ветвей;
 ,
,  и
и  – реактивные проводимости ветвей;
– реактивные проводимости ветвей;
 – комплексная проводимость контура;
– комплексная проводимость контура;
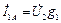 ,
, 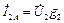 – активные составляющие токов ветвей;
– активные составляющие токов ветвей;
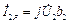 – реактивные составляющие токов ветвей.
– реактивные составляющие токов ветвей.
С учетом  и
и 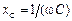 определим проводимости ветвей:
определим проводимости ветвей:


 (6.4)
(6.4)


 (6.5)
(6.5)
Токи  и
и  в параллельных ветвях контура могут во много раз превышать входной ток, поэтому резонанс в параллельном контуре называют резонансом токов. Отношение токов (коэффициент передачи по току) является одной из важных частотных характеристик контура (например, между током через емкость и входным током):
в параллельных ветвях контура могут во много раз превышать входной ток, поэтому резонанс в параллельном контуре называют резонансом токов. Отношение токов (коэффициент передачи по току) является одной из важных частотных характеристик контура (например, между током через емкость и входным током):
 (6.6)
(6.6)
Входное комплексное сопротивление контура:
 (6.7)
(6.7)
Комплексное действующего значения входного тока:
 (6.8)
(6.8)
Комплексная частотная характеристика для схемы рис. 6.1, а:
 (6.9)
(6.9)
С учетом (6.4) и (6.5) можно определить частотные характеристики для параллельного контура:

 (6.10)
(6.10)

 (6.11)
(6.11)

 (6.12)
(6.12)

 (6.13)
(6.13)
При резонансе должно выполняться условие:
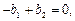
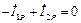 и
и  (6.14)
(6.14)
Из условия (6.14) с учетом  и
и 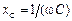 можно определить резонансную частотудля параллельного колебательного контура
можно определить резонансную частотудля параллельного колебательного контура
 , (6.15)
, (6.15)
где  и
и  – резонансная частота и характеристическое сопротивление последовательного контура соответственно.
– резонансная частота и характеристическое сопротивление последовательного контура соответственно.
Как видно из (6.15), резонансная частота 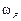 , в отличие от частоты
, в отличие от частоты  , зависит от активных потерь в катушке индуктивности и конденсаторе. Если потери в активных сопротивлениях контура малы:
, зависит от активных потерь в катушке индуктивности и конденсаторе. Если потери в активных сопротивлениях контура малы:  ,
,  то такой контур считается идеальным, а резонансные частоты последовательного и параллельного контура совпадают:
то такой контур считается идеальным, а резонансные частоты последовательного и параллельного контура совпадают:  Анализ выражения (6.15) показывает, что резонанс в контуре происходит при значениях
Анализ выражения (6.15) показывает, что резонанс в контуре происходит при значениях  или
или  при больших же значениях потерь (
при больших же значениях потерь (  ,
,  ) резонанс не наблюдается.
) резонанс не наблюдается.
На резонансной частоте реактивные проводимости ветвей равны между собой  и называются характеристической проводимостьюпараллельного колебательного контура (обратная величина характеристическому сопротивлению
и называются характеристической проводимостьюпараллельного колебательного контура (обратная величина характеристическому сопротивлению 
Отношение действующего значения тока реактивного элемента к входному току параллельного колебательного контура на резонансной частоте называется добротностьюпараллельного колебательного контура:
 (6.16)
(6.16)
На рис. 6.2 показаны частотные характеристики входного сопротивления  и
и  параллельного контура.
параллельного контура.
В резонансном режиме модуль входного сопротивления достигает максимального значения  а у идеального контура его значение равно бесконечности. ФЧХ показывает, что при изменении частоты
а у идеального контура его значение равно бесконечности. ФЧХ показывает, что при изменении частоты  входное сопротивление носит индуктивный характер, а в диапазоне
входное сопротивление носит индуктивный характер, а в диапазоне  – емкостный. Как видно, резонансная частота в параллельном контуре теперь зависит не только от параметров реактивных элементов, но и от значения сопротивлений потерь в ветвях. На ФЧХ входного сопротивления видно, что значения фазы, равные нулю, достигаются при различных значениях частоты.
– емкостный. Как видно, резонансная частота в параллельном контуре теперь зависит не только от параметров реактивных элементов, но и от значения сопротивлений потерь в ветвях. На ФЧХ входного сопротивления видно, что значения фазы, равные нулю, достигаются при различных значениях частоты.
 а
а
|  б
б
|
| Рис. 6.2. Частотные характеристики входного сопротивления параллельного колебательного контура |
На рис. 6.3 показаны частотные характеристики входного то-ка (6.11)  и
и  параллельного колебательного контура.
параллельного колебательного контура.
 а
а
|  б
б
|
| Рис. 6.3. Частотные характеристики тока |
Минимального значения ток достигает при резонансе, а его численное значение  определяется величиной активной проводимости контура.
определяется величиной активной проводимости контура.
На рис. 6.4 показаны характеристики АЧХ и ФЧХ φк(ω) передаточной функции по напряжению, рассчитанные по формулам (6.13) для параллельного контура, включенного последовательно с резистором R (рис. 6.1, а).
 а
а
|  б
б
|
| Рис. 6.4. Частотные характеристики коэффициента передачи по напряжению |
По этим характеристикам может быть определена полоса пропускания, равная разности граничных частот:

Для контуров, имеющих высокое (  >>
>>  и
и  >>
>>  )
)  значение добротности, добротность Q, резонансные частоты последовательного
значение добротности, добротность Q, резонансные частоты последовательного  и параллельного колебательного контуров совпадают
и параллельного колебательного контуров совпадают 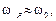 а значение характеристического сопротивления
а значение характеристического сопротивления 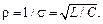
Для увеличения добротности параллельного резонансного контура сопротивление в ветви с конденсатором убирают 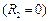 , а в ветви с катушкой индуктивности оставляют только активное сопротивление провода обмотки.
, а в ветви с катушкой индуктивности оставляют только активное сопротивление провода обмотки.
Для расчета частотных характеристик (6.10)–(6.13) контуров с высокой добротностью  и
и  в режиме, близком к резонансу, можно пользоваться приближенными формулами:
в режиме, близком к резонансу, можно пользоваться приближенными формулами:
- входное сопротивление:
 (6.17)
(6.17)
- коэффициент передачи по току:
 (6.18)
(6.18)
где 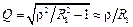 – добротность контура;
– добротность контура;
 обобщенная расстройка;
обобщенная расстройка;
 – резонансная частота.
– резонансная частота.
Добротность контура определяет полосу пропускания:

Для увеличения добротности контура вместо катушек индуктивности используют электронное устройство (гиратор – инвертор сопротивления), выполненное с применением операционных усилителей. Такого рода устройства называются активными фильтрами. Индуктивность гиратора может достигать тысяч Генри при меньших габаритах, по сравнению с обыкновенными катушками индуктивности.
Дата добавления: 2015-04-16; просмотров: 276; Мы поможем в написании вашей работы!; Нарушение авторских прав |