Основные теоретические сведения. Резонансомв электрической цепиили на участке цепи, содержащей конденсаторы и катушки индуктивности, называется явление

Резонансомв электрической цепиили на участке цепи, содержащей конденсаторы и катушки индуктивности, называется явление, при котором гармонические напряжение и ток на входе цепи совпадают по фазе. Существует два вида резонанса: резонанс напряжений в цепи, состоящей из последовательно соединенных конденсатора и катушки индуктивности; и резонанс токов в цепи с параллельным соединением двух ветвей, в одной из которых кроме прочих элементов имеется катушка индуктивности, а в другой – конденсатор. Цепь, в которой наблюдается резонанс напряжений, называется последовательным колебательным контуром. Цепь, в которой наблюдается резонанс токов, называется параллельным колебательным контуром.

Рассмотрим последовательный колебательный контур – участок цепи, состоящей из последовательно соединенных резистора, катушки индуктивности и конденсатора. Ко входу цепи (рис. 5.1) подключен источник гармонического напряжения U₁(t) = U_msin(ωt). Запишем второй закон Кирхгофа в комплексной форме для действующих значений напряжений.

Рис. 5.1. Схема последовательного контура

(5.1)

Пусть .

Уравнение (5.1) позволяет определить токи и напряжения на элементах цепи:

(5.2)

где x_L = ωL;

x_C = 1/(ωC);

X – суммарное реактивное сопротивление ветви;

– комплексное сопротивление ветви;

Z – модуль;

j – аргумент сопротивления.

Из (5.2) можно определить действующее значение тока и его фазу:

Условием резонанса напряжений является равенство реактивных сопротивлений x_L = x_C , ωL = 1/(ωC) или X = 0. При этом условии определяется резонансная частота

(5.3)

На рис. 5.2 показана векторная диаграмма напряжений последовательного контура в режиме резонанса. В этом режиме входной ток достигает максимального значения и его действующее значение составляет Если R является активным сопротивлением проводов катушки, то мощность P = I²R учитывает активные потери мощности в ней. Потери мощности в конденсаторе для низких и средних частот составляют малую величину и в его схеме замещения не учитываются. Действующие значения напряжений на реактивных элементах L и C в режиме резонанса могут значительно превышать входное напряжение:

(5.4)

где – характеристическое сопротивление контура:

(5.5)

Рис. 5.2. Векторные диаграммы напряжений последовательного контура

Отношение Q = ρ/R называется добротностью контура, которая может достигать десятков и даже сотен единиц.

При анализе свойств контура используются частотные характеристики входного сопротивления входного тока а также комплексные передаточные функции для напряжения на катушке индуктивности:

и напряжения на конденсаторе:

С целью оценки свойств электрических цепей используют понятие полосы пропускания (П). Полосой пропускания контура называют диапазон частот, в котором АЧХ изменяется не более чем в раз по сравнению с ее экстремальным (минимальным или максимальным) значением, что соответствует на ЛАЧХ изменению характеристики на 3 дБ.

Из (5.2) получаем частотные характеристики для последовательного колебательного конура.

Зависимости модуля и аргумента комплексного входного сопротивления от частоты:

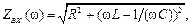
(5.6)

На рис. 5.3 представлены частотные характеристики модуля и аргумента входного сопротивления контура, рассчитанные по формулам (5.6) для двух значений добротности Q. На графиках видно, что входное сопротивление достигает минимального значения при резонансной частоте Z_ВХ = R и максимального – при частотах ω → 0 и ω → ∞.

а	б
Рис. 5.3. АЧХ и ФЧХ входного сопротивления последовательного колебательного контура

Характер входного сопротивления в диапазоне частот 0 ≤ ω ≤ ω₀ является емкостным, а в диапазоне ω₀ ≤ ω ≤ ∞ – индуктивным.

и (5.7)

На рис. 5.4 изображены зависимости действующего значения входного тока и его фазы от частоты, рассчитанные по формулам (5.7) для различных значений добротности Q. Как видно из графиков, ток достигает своего максимального значения при резонансной частоте и нулевого значения при частоте, равной нулю и бесконечности.

а	б
Рис. 5.4. АЧХ и ФЧХ тока колебательного контура

Аналогично (5.7) можно получить выражение для коэффициента передачи по напряжению на конденсаторе:

(5.8)

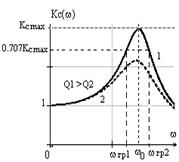
На рис. 5.5 изображены АЧХ, ЛАЧХ и ФЧХ коэффициента передачи по напряжению на конденсаторе.

Полоса пропускания контура (рис. 5.5, б):

(5.9)

где ω_гр1и ω_гр2 – граничные частоты полосы пропускания.

а	б
в
Рис. 5.5. АЧХ, ЛАЧХ и ФЧХ коэффициента передачи по напряжению для конденсатора

На резонансной частоте ФЧХ равна –90°, а с ростом частоты стремится к –180°. На границах полосы пропускания ФЧХ равна –45°и –135°.

Характеристики (5.6)–(5.8) удобно строить в зависимости от относительной частоты ω_ОТ = ω/ω₀ = f/f₀. В (5.6)–(5.8) с учетом характеристического сопротивления и добротности Q

получим

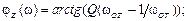(5.10)

(5.11)

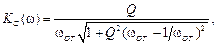
(5.12)

Величина называется обобщенной расстройкой. Для резонансного режима обобщенная расстройка равна нулю . Частотные характеристики чаще строят в функции частоты или ω_ОТ, реже от расстройки .