Круговая диаграмма цепи с постоянным реактивным сопротивлением и переменным активным сопротивлением

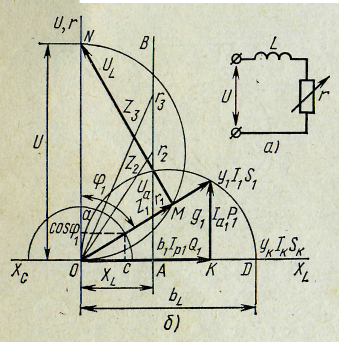Построим круговую диаграмму для цепи, представленной на рис.6.3, а, если индуктивное сопротивление Х_L постоянно, а активное сопротивление г - переменно, т.е. (Х_L= соnst; U = соnst; г — vаг). Активное сопротивление изме­няется от нуля (г = 0, режим корот­кого замыкания) до бесконечности (г = , ре­жим холостого хода).

1. Сначала в произвольном масштабе по вертикальной оси откладывают величину приложенного напряжения U (отрезок ON на рис.6.3, б)

2. По горизонтали вправо откладываем значение X_L (отре­зок OA).

3. Из конца отрезка ОА вверх строим линию активного сопротивле­ния АВ. Если имеются три различных активных сопротивления г₁, г₂, г₃, то полное сопротивление цепи определится как геометриче­ская сумма сопротивлений г, и Х_L, т.е. z₁, z_2, z₃. Прямая АВ является геометри­ческим местом концов векторов полных сопротивлений.

4. Следова­тельно, по теореме об обратных векторах геометрическим местом концов обратных векторов, т. е. полных проводимостей у, будет окружность OD. Согласно правилу обратных векторов центр окружности должен

лежать на горизонтальной оси как на линии, перпендикулярной АВ и проходящей через полюс О. Диаметр окружности OD рассчитывают исходя из условий режима короткого замыкания. При этом учиты­вают только сопротивление Х_L, т.к. наименьшее активное сопротивление г=0.

Следовательно, наибольшая полная проводимость

у_к= = _,

Проводимость, как величину, обратную сопротивлению, откла­дывают в произвольном масштабе по линии соответствующего сопротивления, в данном случае по линии Х_L. На диаграмме у = b_L (отрезок ОD). Точка D, как конец обратного вектора, лежит на окружности. Так как по правилу обратных векторов окружность проходит через полюс О, отрезок ОD соединяет две точки на окруж­ности и проходит через центр, следовательно, он является диамет­ром окружности, по которой скользят концы векторов полных проводимостей. После этого графически определяют полную проводимость для любого заданного активного сопротивления.

5. Полный ток в цепи согласно формуле (6.2)

I = U · y.

Так как U = соnst, ток пропорционален проводимости. Следовательно, все отрезки полных проводимостей являются и отрезками полных токов цепи только в другом масштабе. Под осью проводимостей проводим ось полного тока I. Таким образом, окружность, по которой скользят концы векторов полных проводимостей, является геометрическим местом концов векторов тока.

Масштаб тока определяют по току короткого замыкания

I_к = U · y_к = U · =

На диаграмме ток короткого замыкания характеризуется отрез­ком OD, следовательно, масштаб тока (А/мм).

6. Аналогично можно найти полную мощность цепи: S = U·I

Так как U — соnst, полная мощность цепи пропорциональна полному току.

Следовательно, все отрезки полных токов являются одновременно (в другом масштабе) отрезками полных мощностей цепи. Таким образом, та же окружность с диаметром ОD является геометри­ческим местом концов векторов полных мощностей.

6. Сдвиг фаз между напряжением и током может быть определен графически. Если опустить перпендикуляр из конца отрезка пол­ной проводимости, тока или мощности на ось абсцисс, то получим два отрезка ОК и КL.

Эти отрезки в соответствующих масштабах представляют собой реактивные и активные составляющие прово­димости (b, g), тока (I_р, I_а) и мощности (Q,P).

Построение круговой диаграммы для цепи с емкостным элемен­том аналогично изложенному. Только диаграмма сместится влево от вертикальной оси.