Студопедия

КАТЕГОРИИ:

АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника


Задача 1. Построение топографической векторной диаграммы напряжений неразветвленной цепи.

⇐ ПредыдущаяСтр 17 из 32Следующая ⇒



Рис. 5.1 К построению топографической векторной диаграммы неразветвленной сети.

 

 

Дано: R1=20 Ом;, R2,=20 Ом; L1 = 0,0318 Гн , C1=1,06Е-4 Ф, C2 =2,12Е-4 Ф

1 Определяем значения реактивных сопротивлений ХL, XC для элементов L1, L2, C1, C2 по формулам

XC1 = ; XC2 = ;

ХL1 = ; ХL2 = ,

где ω – циклическая или угловая частота, рад/с;

f – линейная частота, f =50Гц;

L – индуктивность катушки, Гн.

С – емкость конденсатора, Ф.

2 Определяем значения падения напряжения UR, UL, UC, В, на элементах цепи R1, R2, L1, L2, C1, C2 согласно закона Ома

UR1 = I0· R1 ; UR2 = I0· R2;

UL1 = I0· ХL1; UL2 = I0· ХL2;

UC1 = I0· XC1 ; UC2 = I0· XC2.

3 Выбираем масштаб векторной диаграммы значений тока и напряжения.

4 По полученным значениям падения напряжения строимтопографическую векторную диаграмму напряжений, основываясь на следующих принципах:

а) вектор тока I0 откладывают по горизонтальной прямой, так как его начальная фаза равна нулю;

б) вектор URсовпадает по фазе с вектором I;

в) вектор UL откладывают вертикально вверх, так как его фаза равна плюс π/2; 47

г) вектор UС откладывают вертикально вниз, так как его фаза равна минус π/2;

д) результирующий вектор напряжения U как геометрическая сумма всех составляющих:

U = UR1+ UR2 +UC1 +UC2 +UL1 +UL2.

5 На построенной диаграмме графически определяем угол сдвига фаз между вектором тока I0 и результирующим вектором напряжения U - φ.

6 Определяем результирующие активные R и реактивные ХL, XC , полное сопротивления Z цепи по формулам

R = R1 + R2; ХL = ХL1 + ХL2; XC = XC1 + XC2;

Z = .

7 Определяем угол сдвига фаз между током и напряжением

Сosφ = ; Sinφ = .

8 Определяем активную UR, реактивную UL ,UC и полную U составляющую напряжения.

UR = UR1 + UR2; UL = UL1 + UL2; UC = UC1 + UC2; U = .

9 Определяем активную, реактивную и полную мощности цепи

Р = I·U·Cosφ , Вт;

Q = I·U·Sinφ , ВАр;

S = = I·U, В·А

Задача 2. Построение топографической векторной диаграммы токов разветвленной цепи.

10 Определяем активные и реактивные составляющие тока для каждой ветви по формулам

I R1= U0 /R1, I R2= U 0 /R2,

I C1= U 0 /ХС1, I C2= U 0 /ХС2,

I L1= U 0 /ХL1, I L2= U 0 /ХL2,

где R1, R2, ХС1, ХС2, ХL1, ХL2 - параметры определяемые в п.1,2.

11 По полученным значениям тока строимтопографическую векторную диаграмму токов, основываясь на следующих принципах:

а) вектор напряжения U0 откладывают по горизонтальной прямой, так как его начальная фаза равна нулю;

б) вектор IRсовпадает по фазе с вектором U0;

в) вектор IL откладывают вертикально вниз, так как его фаза равна минус π/2;

г) вектор UС откладывают вертикально вверх, так как его фаза равна плюс π/2;

д) результирующий вектор напряжения U как геометрическая сумма всех составляющих:

I = IR1+ IR2 +IC1 +IC2 +IL1 +IL2.

12 Определяем и угол φ между результирующим вектором напряжения U и вектором тока I.

Контрольные вопросы

1. Формулы активного, реактивного и полного сопротивлений.

2. Закон Ома.

3. Определение активной, реактивной и полной мощности цепи.

4. Принципы построения топографической векторной диаграммы токов и напряжений.

5. Понятие коэффициента мощности.

 

Варианты заданий

Задача

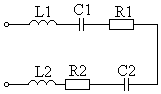
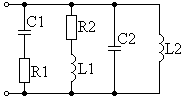
Определить реактивные и полные сопротивления элементов и участков цепи, представленных на схемах (Таблица 5.2). Для неразветвленной цепи определить падение напряжения на элементах схемы и построить векторную диаграмму напряжений. Для разветвленной цепи определить токи, протекающие через ветви цепи и построить векторную диаграмму токов. По построенным диаграммам определить угол сдвига фаз между током и напряжением φ. Номинальные значения представлены в таблице 5.1.

Таблица 5.1 – Номинальные значения элементов схем

 

№ вар № схемы R1, Ом R2, Ом C1, Ф C2, Ф L1, Гн L2, Гн Для задачи1 I0,A Для задачи2 U0,B
1. 0,000318 0,000212 0,031847 0,047771
2. 0,000637 0,000265 0,015924 0,038217
3. 0,000159 0,000106 0,063694 0,095541 0,5
4. 7,96Е-05 6,37Е-05 0,127389 0,159236 0,2
5. 0,000127 9,1Е-05 0,079618 0,111465 0,4
6. 5,79Е-05 7,08Е-05 0,175159 0,143312
7. 3,54Е-05 3,18Е-05 0,286624 0,318471 0,1
8. 5,31Е-05 7,96Е-05 0,191083 0,127389 2,5
9. 6,37Е-05 4,55Е-05 0,159236 0,22293 1,5
10. 0,000106 0,000212 0,095541 0,047771 0,6
11. 3,98Е-05 3,18Е-05 0,254777 0,318471 0,8
12. 0,000265 0,000159 0,038217 0,063694 2,4
13. 7,08Е-05 0,000127 0,143312 0,079618 1,1
14. 5,31Е-05 5,79Е-05 0,191083 0,175159 3,2
15. 0,000127 4,25Е-05 0,079618 0,238854 2,5
16. 9,1Е-05 5,31Е-05 9,1Е-05 0,191083 0,4
17. 6,37Е-05 7,96Е-05 0,159236 0,127389 1,6
18. 4,9Е-05 0,000106 0,207006 0,095541 0,5
19. 4,55Е-05 3,98Е-05 0,22293 0,254777 0,4
20. 4,25Е-05 0,000127 0,238854 0,079618 0,2
21. 3,18Е-05 3,54Е-05 0,318471 0,286624 0,1
22. 0,000159 0,000106 0,063694 0,095541 1,4
23. 7,96Е-05 5,79Е-05 0,127389 0,175159 2,4
24. 0,000127 6,37Е-05 0,079618 0,159236 2,6
25. 0,000212 9,1Е-05 0,047771 0,111465 0,7
26. 3,98Е-05 3,18Е-05 0,254777 0,318471 0,3
27. 4,9Е-05 7,96Е-05 0,207006 0,127389 0,2
28. 6,37Е-05 4,25Е-05 0,159236 0,238854
29. 9,1Е-05 0,000212 9,1Е-05 0,047771 3,5
30. 3,98Е-05 3,18Е-05 0,254777 0,318471 0,25
31. 7,96Е-05 6,37Е-05 0,127389 0,159236 0,8
32. 0,000127 6,37Е-05 0,079618 0,159236 1,5
33. 5,79Е-05 7,08Е-05 0,175159 0,143312
34. 3,54Е-05 3,18Е-05 0,286624 0,318471 2,5
35. 4,9Е-05 7,96Е-05 0,207006 0,127389

 

 

Таблица 5.2 - Варианты схем

№ Задача 1 Задача 2

 

 

 

Поделиться:

Дата добавления: 2015-04-16; просмотров: 116; Мы поможем в написании вашей работы!; Нарушение авторских прав

⇐ Предыдущая12131415161718192021Следующая ⇒
lektsii.com - Лекции.Ком - 2014-2024 год. (0.005 сек.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав
Главная страница Случайная страница Контакты