Круговая диаграмма цепи с постоянным активным, реактивным сопротивлением и переменным активным сопротивлением

Построим круговую диаграмму для цепи с постоянным активным г_к и реактивным Х_L сопротивлениями и переменным активным сопротивлением г, т.е. г_к = соnst; и U = соnst; Х_L= соnst; г = vаг, представленной на рис. 6.5, а. При этом активное сопротивле­ние изменяется от нуля (г = 0, режим короткого

замыкания) до бесконечности (г = , режим холостого хода). Методика построения таких диаграмм аналогична ранее изло­женному, поэтому укажем лишь основные моменты построения.

Сначала откладывают все известные постоянные параметры: отрезок ON — напряжение U, отрезок ОА— индуктивное сопро­тивление Х_L, отрезок АК— постоянное активное сопротивление г_к,отрезок ОК — полное сопротивление Z_К. Из точки К проведем верти­кальную линию активного сопротивления КВ. Зададимся некото­рым активным сопротивлением г. Тогда полное сопротивление цепи определится как геометрическая сумма сопротивлений Х_L, г_к, г . Таким образом, линия АКВесть прямая, по которой скользят концы векторов полных сопротивлений Z. Концы векторов полных проводимостей у будут скользить по окружности.

Центр окружности определим в режиме короткого замыкания цепи (г =0). При этом проводимость

у_к= = _.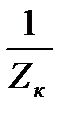

В режиме короткого замыкания величину проводимости откла­дываем в произвольном масштабе по линии ОК(отре­зок ОD). Хотя точка Dлежит на окружности проводимостей, а от­резок ОDхарактеризует максимальную проводимость данной цепи, тем не менее он не является диаметром окружности скольжения концов векторов полных проводимостей, так как по правилу обрат­ных векторов центр такой окружности должен находиться на пря­мой, перпендикулярной линии скольжения прямых векторов. Чтобы определить этот центр, восставим перпендикуляр из точки Dк отрезку ОDдо его пересечения с горизонтальной осью. Отрезок ОСи есть диаметр окружности, по которой скользят концы векторов полных проводимостей. Задаваясь любыми значениями г, можно определять соответствующие проводимости цепи.

Линию проводимости ОD в режиме короткого замыкания называют линией раздела мощности. Отрезок m₁f₁определяет активную мощность Р'₁, развиваемую на переменном активном со­противлении г.

Ордината, определяющаяся отрезком n₁f₁, есть активная мощ­ность Р_к, развиваемая на постоянном активном сопротивлении г_к. Суммарная ордината есть активная мощность, развиваемая всей цепью: Р'₁+ Р_к= Р₁.

Отрезок ОМпредставляет собой активное напряжение цепи U_a, т. е. активное напряжение постоянного элемента и активное напря­жение переменного элемента цепи. Отрезок MN является реактивное напряжение цепи U_L.