
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теорема Фурье
Всякая периодически изменяющаяся функция (э. д. с, напряжение, ток) может быть разложена в ряд, первый член которого есть величина постоянная, не зависящая от времени, а все остальные являются синусоидальными функциями с кратными частотами:
f(х)=A0+A1Sin(ωt+  )+A2Sin(2ωt+
)+A2Sin(2ωt+ 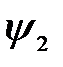 )+A3Sin(3ωt+
)+A3Sin(3ωt+  )+ . . ., (7.1)
)+ . . ., (7.1)
где f(х)- периодически изменяющаяся несинусоидальная функция;
А0- постоянная составляющая; А1,А2,А3- амплитуды синусоидально изменяющихся функций;  ,
, 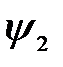 ,
,  -начальные фазы синусоидальных функций.
-начальные фазы синусоидальных функций.
На рис.7.1 (а—в) приведены кривые несинусоидальных э. д. с. (сплошные линии), образованные двумя синусоидальными составляющими (пунктирные линии).
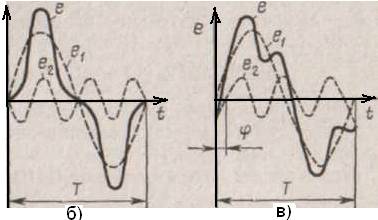
| Рис.7.1. Кривые несинусоидальных э. д. с |
Кривые на рис.7.1 а—в отличаются друг от друга амплитудами, частотой и фазой. Для рис. 7.1, а) е = Eml sin ωt - Em3 sin3ωt;
б)е = Eml sin ωt + Еm3 sin (З ωt — π); в) е = Eml sin ωt – Еm3 sin (З ωt — φ3).
Синусоидальные члены ряда называют гармоническими составляющими или просто гармониками. Первую гармонику, частота которой равна частоте заданной несинусоидальной функции называют первой или основной гармоникой, а
остальные гармоники частота которых в два, три и более раза больше частоты основной гармоники, называют высшими.
Каждая из высших гармоник носит название, соответствующее кратности ее частоты. Например, гармонику, частота которой в два раза больше частоты основной гармоники, называют второй, гармонику, частота которой в три раза больше частоты основной гармоники, — третьей и т. д.
СИММЕТРИЧНЫЕ ПЕРИОДИЧЕСКИЕ НЕСИНУСОИДАЛЬНЫЕ
ФУНКЦИИ
| Рис. 7.2 График функции, симметричной относительно оси абсцисс |
 В электрических машинах напряжение, ток, э. д. с. и т. д. являются функциями периодическими несинусоидальными, но симметричными. Такие функции обладают определенными свойствами.
В электрических машинах напряжение, ток, э. д. с. и т. д. являются функциями периодическими несинусоидальными, но симметричными. Такие функции обладают определенными свойствами.
Функция, симметричная относительно оси абсцисс показана на рис.7.2 При этом функция обладает свойством.
f (x) = -f ( x - π ),
т.е.значение функции повторяется с обратным знаком через половину периода.
Функция, симметричная относительно начала ординат имеет свойство
f (x) = -f (x),
Такая функция не содержит постоянной составляющей (А 0) и содержит только синусоидальные составляющие.
ДЕЙСТВУЮЩИЕ ЗНАЧЕНИЯ НЕСИНУСОИДАЛЬНОГО ТОКА И НАПРЯЖЕНИЯ
Как известно, действующие значения переменного тока или напряжения определяются выражениями
I=  ; U=
; U=  (7.2)
(7.2)
или I=  , U=
, U=  (7.3)
(7.3)
Несинусоидальная функция тока (напряжения) характеризуется коэффициентом искажения. Коэффициентом искажения называют отношение действующих значений основной (первой) гармоники и всей функции:
ki=  , ku=
, ku= 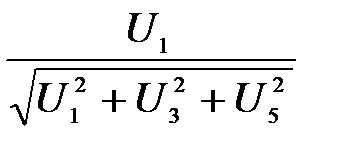 (7.4)
(7.4)
Следует заметить, что коэффициент искажения функции напряжения не равен коэффициенту искажения функции тока. Чем меньше коэффициент искажения отличается от единицы, тем ближе к синусоиде данная кривая.
МОЩНОСТЬ ЦЕПИ ПРИ НЕСИНУСОИДАЛЬНОМ ТОКЕ
При отсутствии постоянных составляющих полную мощность определяют как произведение действующих значений напряжения и тока
S=I·U=  ∙
∙  (7.5)
(7.5)
Дата добавления: 2015-04-16; просмотров: 399; Мы поможем в написании вашей работы!; Нарушение авторских прав |