
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задание. К цепи, показанной на рисунке 7.3, подведено несинусоидальное напряжение
| Рис. 7.3 |
 К цепи, показанной на рисунке 7.3, подведено несинусоидальное напряжение. Определить уравнение токов действующее значение тока I и напряжения U, мощности цепи S, а также коэффициенты искажения тока kI и напряжения kU, если известно С, L, R, f = 50 Гц.
К цепи, показанной на рисунке 7.3, подведено несинусоидальное напряжение. Определить уравнение токов действующее значение тока I и напряжения U, мощности цепи S, а также коэффициенты искажения тока kI и напряжения kU, если известно С, L, R, f = 50 Гц.
План расчета
1. Определяем индуктивное сопротивление цепи для первой, третьей и пятой гармоник по формуле (5.2):
XLk=k·ω·L, (7.6)
т.е. XL1=ω1·L , XL3=3·ω·L, XL5=5·ω·L.
2. Определяем емкостное сопротивление цепи для первой, третьей и пятой гармоник по формуле (5.3):
XCk=  , (7.7)
, (7.7)
т.е. XC1=  , XC3=
, XC3=  , XC5=
, XC5=  .
.
3. Определяем полное сопротивление цепи для каждой гармоники
Z=  , (7.8)
, (7.8)
т.е. Z1= 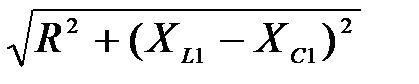 , Z3=
, Z3= 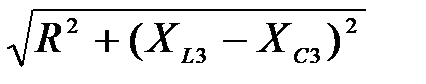 , Z5=
, Z5= 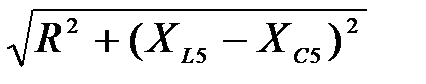
4. Определяем амплитуды токов гармоник
Im=  , (7.9)
, (7.9)
т.е. Im1= 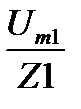 ,Im3=
,Im3=  ,Im5=
,Im5=  , гдеUm1, Um3,Um5 – амплитуды, определяемые из заданного уравнения.
, гдеUm1, Um3,Um5 – амплитуды, определяемые из заданного уравнения.
5. т.к. для всех гармоник реактивные сопротивления различны, а активные сопротивления неизменны, то сдвиг фаз φ для каждой гармоники находят по формуле
tgφ=  , (7.10)
, (7.10)
т.е. tgφ1= 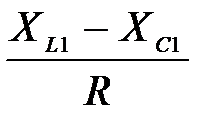 tgφ3=
tgφ3=  tgφ5=
tgφ5= 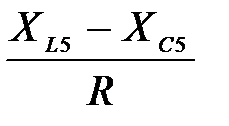
необходимо учитывать: если tg φ имеет знак «+», то напряжение опережает ток, если «-» - ток опережает напряжение.
По таблице 7.1 определяем угол φ.
Таблица 7.1 – Значения тригонометрических функций
| φ | tgφ | φ | tgφ | φ | tgφ | φ | tgφ | φ | tgφ |
| 0,7 | 2,75 | -3,73 | -0,7 | ||||||
| 0,09 | 0,84 | 3,73 | -2,75 | -0,58 | |||||
| 0,18 | 5,67 | -1,73 | -0,47 | ||||||
| 0,27 | 1,19 | 11,43 | -1,43 | -0,36 | |||||
| 0,36 | 1,43 | -1,19 | -0,27 | ||||||
| 0,47 | 1,73 | -11,43 | -1 | -0,18 | |||||
| 0,58 | 2,14 | -5,67 | -0,84 |
6. Записываем уравнение для мгновенного значения тока в цепи:
i=i1+i3+i5= Im1Sin(ω1t+φ1)+ Im3Sin(ω3t+φ3)+ Im5Sin(ω5t+φ5) (7.11)
7. Определяем действующие значения силы тока I и напряжения U
Imk=  , Umk=
, Umk= 
I= 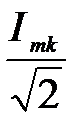 ; U=
; U= 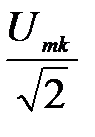 ; (7.12)
; (7.12)
8.Определяем мощность цепи при несинусоидальном токе (при отсутствии постоянной составляющей)
S=I·U=  ·
·  , (7.13)
, (7.13)
9. Определяем коэффициент искажения тока и напряжений
ki=  , ku=
, ku=  (7.14)
(7.14)
10. Строим график мгновенного значения несинусоидального напряжения.
U=Um1Sin(ω1t+φ1)+ Um3Sin(ω3t+φ3)+ Um5Sin(ω5t+φ5) (7.15)
7.5 Пример расчёта и графическое построение периодических
Дата добавления: 2015-04-16; просмотров: 248; Мы поможем в написании вашей работы!; Нарушение авторских прав |