
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод преобразования
Этот метод состоит в замене групп последовательно и параллельно соединенных резисторов эквивалентным Rэ Затем по уравнению состояния простого контура находят ток в неразветвленной части цепи. Посредством обратного преобразования находят токи во всех ветвях заданной цепи.
ПРИМЕР
В электрической схеме рис. 10, а эквивалентное сопротивление Rэ =Rв+R1 +R2 +R34, где R34 = R3R4/(R3+R4) Ток в неразветвленной части схемы I = E/Rэ Токи в ветвях и напряжение на участке U34: I3 = U34/R3; I4 = U34/R4;
U34= Е- U13 = E-(Rв+ R1 +R2)I или U34=R34I; I3=IR4/(R3+R4); I4=R3/(R3 + R4).
На рис. 10,б приведена более сложная схема, в которой прямую замену замыкающихся на разные узлы резисторов эквивалентным сопротивлением произвести нельзя. Здесь резисторы R4,R5 и R6 образуют треугольник (∆), а сопротивления R2, R4 и R5 образуют звезду (Y). Для расчета схемы в этом случае можно воспользоваться уравнениями состояния узла и контура
или преобразовать треугольник в звезду (рис. 10, в). Тогда схема значительно упростится.


ЗАПОМНИТЕ
Сопротивление луча эквивалентной звезды равно произведению сопротивления сторон треугольника, прилегающих к лучу, деленному на сумму сопротивлений всех сторон треугольника. Для замены звезды эквивалентным треугольником пользуются следующими формулами:
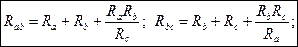

ЗАПОМНИТЕ
Здесь сопротивление стороны треугольника равно сумме сопротивлений двух лучей звезды, опирающихся на это сопротивление, плюс произведение сопротивлений указанных лучей, деленное на сопротивление третьего луча звезды. Возвращаясь к схеме рис. 10,б, после преобразования треугольника R4R5R6 в звезду, получим двухконтурную схему:

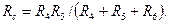
Дата добавления: 2015-04-16; просмотров: 283; Мы поможем в написании вашей работы!; Нарушение авторских прав |