Методы анализа режимов отдельной ветви или части электрической цепи

В практике возникает необходимость исследовать режимы отдельных участков или ветвей схемы при изменении их параметров или параметров на других участках (ветвях) схемы, выбрать оптимальные режимы их работы, например при максимальной мощности, заданном коэффициенте полезного действия, получении линейности и стабильности характеристики при изменении режимов источника питания и др.

►Воздействие сложной активной электрической цепи (активного двухполюсника) на исследуемую ветвь можно заменить воздействием последовательно соединенных эдс E_э и его внутреннего сопротивления R_в. Докажем возможность такой замены, выделив ветвь с сопротивлением R (рис. 12, а).

Включим в исследуемую ветвь последовательно и встречно две одинаковые эдс Е_x и ,равные напряжению холостого хода U_x при разрыве ветви с R. В этом случае ток в этой ветви I остается неизменным (рис. 12, б). Если теперь использовать

принцип наложения, рассматривая две схемы (рис. 12, в), то ток ветви cd будет определяться только правой схемой, характеризуемой эдс холостого хода Е_х, направление которой совпадает с направлением тока в исходной схеме, и внутренним (входным) сопротивлением R_в двухполюсника. Таким образом, ток ветви cd равен действительному току:

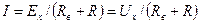
В частности, при R = 0 (короткое замыкание ветв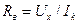и)

и

Если рассматриваемая ветвь содержит источник эдс Е , то ток в ней

где эдс Е берется с плюсом, когда напряжение U_х и эдс Е действуют в одном направлении, и с минусом, когда эдс Е направлена навстречу U_х. Этот метод анализа называют методом эквивалентного источника.

Метод используется и в тех случаях, когда необходимо проанализировать режим одной ветви разветвленной электрической цепи при изменении параметров в другой ветви. Характерным примером такой цепи является схема мостового преобразователя (схема моста), представленная на рис. 13. Ветви, соединяющие соседние узлы а и с, с и b, b и d, d и а, называют плечами моста. Они содержат резистивные элементы. Ветвь ab является диагональю питания моста. В эту ветвь включен источник Е. Ветвь cd содержит измерительный прибор. Эту ветвь моста называю' измерительной диагональю.

Мост можно привести в состояние равновесия, которое насту пает при равенстве падений напряжений на плечах ас и ad, т. е при R₁I₁ = R₄I₄ и R₂I₂= R₃I₃ или, что то же, V_a — V_c = V_a — V_b В момент равновесия потенциалы узлов c и d равны (V_c= V_d) и ток I₅ в диагонали cd равен нулю (стрелка измерительной прибора установится на нулевой отметке). В этом случае I₁ = I₂ и I₃=I₄. Условие равновесия моста:

или

Равновесие моста будет нарушено, если в каком-либо плече моста изменится сопротивление. Тогда изменятся токи в ветвях, изменятся потенциалы узлов с и d(V_c≠V_d). В диагонали cd появится ток, и стрелка прибора отклонится от нулевого положения. Такой мост называется неуравновешенным.

ПРИМЕР Рассмотрим, как определяется ток в ветви с измерительным прибором, сопротивление которого равно R_П, при изменении сопротивления R₁. Решение задачи проводится методом эквивалентного источника, согласно которому ток I₅ определяется по формуле I5= U_cd/(R_в-R_П), где U_cd — напряжение между точка ми с и d при R_П =∞ (разрыв цепи измерительного прибора); R_в — внутреннее ее сопротивление моста относительно зажимов cd.

Для определения зависимости I₅(R₁) необходимо подсчитать R_в и U_cd:

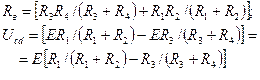
Задаваясь значениями R₁, определяют значения U_cd и R_в. По полученным значениям U_cd и R_в находят значения I₅ и строят зависимость I₅(R₁).