Расчет трехфазных цепей

Расчет трехфазных трехпроводных электрических цепей в несимметричном режиме производится комплексным методом, так как в этом режиме токи и напряжения фаз не равны между собой и основные соотношения между линейными и фазными величинами не выполняются.

Пример расчета трехфазной цепи при соединении нагрузки звездой:

Заданна схема трехфазной трехпроводной цепи (рис. 2.7), с соединением нагрузки звездой и сопротивления фаз нагрузки:

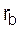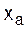, Ом	, Ом	, Ом	, Ом	, Ом	, Ом

Рис. 2.7. Схема трехфазной цепи с нагрузкой, соединенной звездой

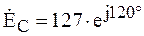Нагрузка несимметричная, ЭДС трехфазного идеального источника равны: В, , В.

По заданным значениям активных и реактивных сопротивлений фаз нагрузки определить: фазные токи и напряжения на нагрузке, напряжение смещения нейтрали, активную, реактивную, полную мощность.

Решение:

В несимметричном режиме работы трехпроводной трехфазной цепи, с нагрузкой, соединенной звездой, возникает напряжение смещения нейтрали . Величину этого напряжения можно определить по методу двух узлов. При известных комплексных сопротивлениях и проводимостях фаз нагрузки:

См,

Ом;

См;

Ом;

См;

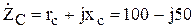Ом.

Напряжение смещения нейтрали определяется по формуле:

Фазные напряжения на нагрузке в несимметричном режиме определяются по второму закону Кирхгофа:

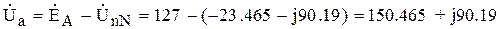В;

Фазные токи нагрузки равны линейным токам и определяются по формулам:

А;

А;

А.

Сумма фазных токов, по первому закону Кирхгофа, должна быть равна нулю:

.

Комплекс полной мощности трехфазной нагрузки, соединенной звездой:

где: - сопряженные комплексы фазных токов.

Активная мощность Р = 476.426 Вт, а реактивная мощность Q = 59.553 ВА.

Пример расчета трехфазной цепи при соединении нагрузки треугольником:

Заданна схема трехфазной трехпроводной цепи (рис. 2.8), с соединением нагрузки треугольником и сопротивления фаз нагрузки:

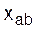, Ом	, Ом	, Ом	, Ом	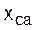, Ом	, Ом

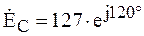Нагрузка несимметричная, ЭДС трехфазного идеального источника равны: В, , В.

По заданным значениям активных и реактивных сопротивлений фаз нагрузки определить: фазные токи и напряжения на нагрузке, фазные напряжения на нагрузке, активную, реактивную, полную мощность.

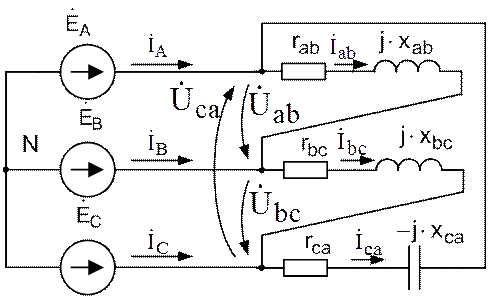
Рис. 2.8. Схема трехфазной цепи при соединении нагрузки треугольником

Решение:

В несимметричном режиме работы трехпроводной трехфазной цепи, с нагрузкой, соединенной треугольником, фазные напряжения на нагрузке равны линейным напряжениям источника питания. Величины этих напряжений можно определить по второму закону Кирхгофа:

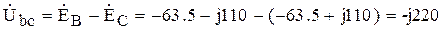В;

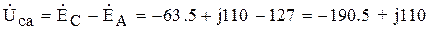В;

В.

При известных комплексных сопротивлениях фаз нагрузки:

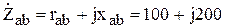Ом;

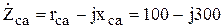Ом;

Ом.

Фазные токи рассчитываются по закону Ома:

А;

А;

А.

Линейные токи определяются по первому закону Кирхгофа:

А;

А;

А.

Сумма линейных токов, по первому закону Кирхгофа, должна быть равна нулю: .

Комплекс полной мощности трехфазной нагрузки, соединенной треугольником:

где: - сопряженные комплексы фазных токов.

Активная мощность Р = 338.709 Вт, а реактивная мощность Q = 435.483 ВА.