Функциональные устройства на операционных усилителях

Современные цифровые вычислительные машины позволяют с высокой точностью выполнять широкий круг математических операций с числами. Однако в измерительных и управляющих системах величины, подлежащие обработке, как правило, представляют собой непрерывные сигналы, например, изменяющиеся значения электрического напряжения. В этих случаях приходится применять аналого-цифровые и цифро-аналоговые преобразователи. Такой подход оправдывает себя только тогда, когда требования к точности вычислений настолько высоки, что не могут быть обеспечены с помощью аналоговых вычислителей. Существующие аналоговые вычислители позволяют получить погрешность порядка 0,1 %. Ниже рассмотрены наиболее важные аналоговые вычислительные схемы на ОУ. Обычно полагается, что операционные усилители являются идеальными. При высоких требованиях к точности выполнения математических операций необходимо учитывать также свойства реальных усилителей.

Схема суммирования. Для суммирования нескольких напряжений можно применить операционный усилитель в инвертирующем включении. Входные напряжения через добавочные резисторы подаются на инвертирующий вход усилителя (рис. 2.22). Поскольку эта точка является виртуальным нулем, то на основании первого закона Кирхгофа при нулевых входных токах идеального ОУ получим следующее соотношение для выходного напряжения схемы:

U_вых / R_S = -(U₁/R₁ + U₂/R₂ + ... + U_n/R_n).

Рис. 2.22 Схема инвертирующего сумматора

Рис. 2.23 Схема инвертирующего интегратора

Схема интегрирования. Весьма важное значение для аналоговой вычислительной техники имеет применение операционных усилителей для реализации операций интегрирования. Как правило, для этого используют инвертирующее включение ОУ (рис. 2.23).

По первому закону Кирхгофа с учетом свойств идеального ОУ следует для мгновенных значений: i₁ = - i_c. Поскольку i₁ = u₁/R₁, а выходное напряжение схемы равно напряжению на конденсаторе

,

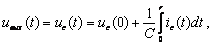то выходное напряжение определяется выражением:

.

Постоянный член u_вых (0) определяет начальное условие интегрирования. С помощью схемы включения, показанной на рис. 2.24, можно реализовать необходимые начальные условия. Когда ключ S1 замкнут, а S2 разомкнут, эта схема работает так же, как цепь, изображенная на рис.2.24. Если же ключ S1 разомкнуть, то зарядный ток при идеальном ОУ будет равен нулю, а выходное напряжение сохранит значение, соответствующее моменту выключения. Для задания начальных условий следует при разомкнутом ключе S1 замкнуть ключ S2. В этом режиме схема моделирует инерционное звено и после окончания переходного процесса, длительность которого определяется постоянной времени R₃C, на выходе интегратора установится напряжение

U_вых = -(R₃ / R₂)U₂ (2.6)

После замыкания ключа S1 и размыкания ключа S2 интегратор начинает интегрировать напряжение U₁, начиная со значения (2.6).

Рис. 2.24 Интегратор с цепью задания начальных условий

Схема дифференцирования. Поменяв местами резистор и конденсатор в схеме интегратора на рис. 2.23, получим дифференциатор (рис. 2.25). Применение первого закона Кирхгофа для инвертирующего входа ОУ в этом случае дает следующее соотношение:

C(dU_вх /dt) + U_вых /R = 0

или

U_вых = – RC(dU_вх /dt).

Рис. 2.25 Схема дифференциатора

Используя формулу

и учитывая, что в схеме на рис. 2.25 вместо R₁ используется 1/sC, a R₂=R, найдем передаточную функцию дифференциатора

K(s) = -sRC.

Подставив s = jω, получим частотную характеристику дифференциатора

K(jω) = -jωRC,

модуль которой |K| = ωRC пропорционален частоте.