
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Функции в алгебре логики
Функции и аргументы в алгебре логики определены на множестве {0, 1} и, следовательно, могут принимать только два значения. Как и в обычной алгебре, функции и аргументы обозначаются буквами выбранного алфавита. Все возможные комбинации значений аргументов называются наборами. Число наборов для N аргументов составляет 2N. На каждом наборе аргументов функция может принимать два значения, следовательно, для N аргументов можно получить 22N различных функций.
Рассмотрение понятия функции в алгебре логики (АЛ) можно начать с функций одной переменной х(N = 1). Она имеет 21 = 2 набора (0 и 1) и соответственно четыре функции yi (табл. 3.1).
Таблица 3.1
Функции одной переменной в АЛ
| Переменная | Функции | |||
| x | y1 | y2 | y3 | y4 |
Очевиден и содержательный смысл этих функций: y1 – константа нуля, y2 – повторение x, y3 – инверсия, x и y4 – константа единицы.
Для двух переменных может быть введено уже 16 функций (табл. 3.2). В табл. 3.3 дано условное обозначение логических элементов, реализующих эти функции.
Таблица 3.2
Функции двух переменных в АЛ
| Переменные | x1 | ||||
| x2 | |||||
| Функции | |||||
| f0 | |||||
| f1 | |||||
| f2 | |||||
| f3 | |||||
| f4 | |||||
| f5 | |||||
| f6 | |||||
| f7 | |||||
| f8 | |||||
| f9 | |||||
| f10 | |||||
| f11 | |||||
| f12 | |||||
| f13 | |||||
| f14 | |||||
| f15 |
Функции двух переменных, рассмотренные в табл. 3.3, играют важную роль в алгебре логики и могут быть названы элементарными (рис 3.1).
К элементарным функциям обычно относят: функцию инверсии (отрицания), конъюнкцию, дизъюнкцию, импликацию, штрих Шеффера и стрелку Пирса.
Таблица 3.3.
Содержательная таблица функций двух переменных в АЛ
| Функция в аналитическом выражении | Наименование | Словесное выражение | Выражение в элементарном базисе | Функциональное обозначение |
| f0=0 | Константа “0” | Всегда ложно | 
| см.рис. 3.1, а |
| f1=x1&x2 | Конъюнкция, И | x1 и x2 | 
| см.рис. 3.1, б |
f2=x1  x2 x2
| Запрет x1 | Запрет по x2 | 
| см.рис. 3.1, в |
| f3=x1 | Повторение x1 | Повторение x1 | 
| см.рис. 3.1, г |
f4=x2  x1 x1
| Запрет x2 | Запрет по x1 | 
| см.рис. 3.1, д |
| f5=x2 | Повторение x2 | Повторение x2 | 
| см.рис. 3.1, е |
| f6=x1Åx2 | Исключающее ИЛИ | x1 неравнозначно x2 | 
| см.рис. 3.1, ж |
| f7=x1v x2 f7=x1+x2 | Дизъюнкция, ИЛИ | x1 или x2 | 
| см.рис. 3.1, з |
| f8=x1↓x2 | Стрелка Пирса, ИЛИ-НЕ | Отрицание дизъюнкции | 
| см.рис. 3.1, и |
| f9=x1~x2 | Равнозначность, эквивалентность | x1 равнозначно x2 | 
| см.рис. 3.1, к |
| f10=x2 | Инверсия, отрицание x2 | Не x2 | 
| см.рис. 3.1, л |
f11=x2  x1 x1
| Импликация x1 | Если x2, то x1 | 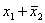
| см.рис. 3.1, м |
| f12=x1 | Инверсия, отрицание x1 | Не x1 | 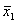
| см.рис. 3.1, н |
f13=x1  x2 x2
| Импликация x2 | Если x1, то x2 | 
| см.рис. 3.1, о |
| f14=x1 x2 | Штрих Шеффера, И-НЕ | Отрицание конъюнкции | 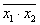
| см.рис. 3.1, п |
| f15=1 | Константа “1” | Всегда истинно | 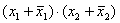
| см.рис. 3.1, р |

Рис 3.1 Обозначение логических элементов
Для трёх переменных существует уже 23 = 8 наборов, дающих 256 логических функций. С целью получения новых функций можно использовать принцип суперпозиции, позволяющий подставлять одни функции вместо аргументов в другие функции. При этом возникает вопрос – какой номенклатурой логических элементов можно ограничиться, чтобы можно было реализовывать любые, сколь угодно сложные функции.
Система булевых функций называется функционально-полной, если произвольная булева функция вида f (x1, x2, ..., xn) может быть представлена суперпозицией конечного числа функций системы, а набор элементов реализующих данные функции – функционально полным набором или базисом.
В качестве простейших принято рассматривать следующие пять базисов:
1) дизъюнкция (xivxj), конъюнкция (xi&xj), инверсия (  );
);
2) дизъюнкция (xivxj), инверсия (  );
);
3) конъюнкция (xi&xj), инверсия (  );
);
4) стрелка Пирса (xi ↓xj =  );
);
5) штрих Шеффера (xi xj =  ).
).
С точки зрения практической реализации булевых функций функциональная полнота этих базисов показывает, что произвольная логическая цепь, включая и ЭВМ, может быть построена из простых функциональных элементов, вплоть до случая элементов одного типа (например, Пирса или Шеффера). В действительности электронной промышленностью выпускается ограниченный, но заведомо избыточный набор логических элементов, что позволяет сократить общее число микросхем в конкретном логическом блоке за счет расширения номенклатуры.
Дата добавления: 2015-04-16; просмотров: 355; Мы поможем в написании вашей работы!; Нарушение авторских прав |