Минимизация булевых функций.

Минимизация функций алгебры логики– это процедура нахождения наиболее простого их представления в виде суперпозиции функций, составляющих функционально полную систему, при одновременной оптимизации ее технической реализации по некоторым критериям в условиях ряда ограничений. Критериями оптимизации могут быть объем оборудования (количество вентилей, корпусов), габариты, вес, энергопотребление, стоимость, быстродействие, надежность. Существует достаточно много методов упрощения, здесь будут рассмотрены три основных метода: с использованием карт Карно, избыточных комбинаций и для системы нескольких функций.

Для упрощения можно использовать как непосредственно аксиомы алгебры логики, так и специальные приемы. Произведем упрощение выражения для F на основе аксиом:

Однако такой метод не имеет достаточной наглядности, а также требует опыта и интуиции. Поэтому чаще используют более формализованные методы упрощения.

Метод карт Карно. Карта Карно является специальной формой таблицы истинности функции, позволяющей не только её задать, но и выполнить минимизацию. Карта содержит 2ⁿ клеток для всех возможных сочетаний переменных и их инверсий, причём каждой клетке соответствует строго определённый минтерм. Так, для трёх переменных А, В и С карта содержит 2³ = 8 клеток, а для четырех переменных – 2⁴ = 16, и имеет вид, показанный на рис. 3.3.

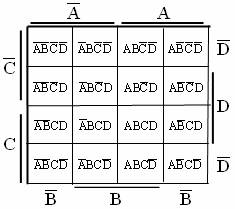
Рис. 3.3 Карта Карно для четырёх переменных

Обычно в клетки карты заносят не сами минтермы, а метят единицами клетки, соответствующие этим минтермам. Правила минимизации с использованием карт Карно заключаются в следующем:

1) В карту Карно заносится исходная функция. Для этого метятся единицами клетки, соответствующие присутствующим в этой функции минтермам. Если на одну и ту же клетку приходится несколько единиц, то она метится лишь один раз.

2) Соседние, помеченные единицами клетки обводятся контурами («склеива-ются»). Контур склейки должен иметь форму квадрата или прямоугольника и содержать число клеток 2ⁱ (i = 0, 1, 2,...n).

3) Одни и те же клетки можно обводить сколько угодно раз.

4) При проведении контуров крайние строки карты (верхние и нижние, левые и правые), а также угловые клетки считаются соседними (для карт до четырех переменных).

5) Каждый контур должен включать максимально возможное количество клеток, а число контуров должно быть минимальным.

6) Функция выписывается из контуров карты. Переменная, входящая в контур как в прямом, так и в переменном виде, поглощается (см. закон поглощения).

7) Все единицы в карте (даже одиночные) должны быть охвачены контурами.

Принцип минимизации заключается в объединении соседних полей карты в пределах правильных конфигураций. При нахождении минимальной формы ФАЛ, выписываются переменные, не изменяющие своего значения в пределах склейки

Рис. 3.4 Диаграмма минимизации функции F

Пример минимизации приведённой выше функции F методом Карт Карно представлен на рис. 3.4. Значения 0 либо 1 над клетками карты указывают, в каких полях карты ложны либо истинны значения Х₁ либо Х₂.

Запись функции F заключается в занесении единиц в клетки карты, соответствующие минтермам этой функции. Для данного случая можно построить три контура, содержащих по две клетки. Искомое минимизированное выражение есть логическая сумма укороченных произведений переменных, имеющих одно значение в пределах контура, без переменных, имеющих оба возможных значения (0 и 1) в пределах контура. Таким образом, согласно рис. 3.4, будем иметь

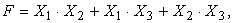
где первый член дает вертикальный контур, второй член – правый горизонтальный контур, и третий член определяется левым горизонтальным контуром.

После этого можно уже составлять функциональную схему, выполняющую операцию F (рис. 3.5).

Рис. 3.5 Схема реализации упрощённой функции F   Использование избыточных комбинаций. При проектировании случается, что определенные комбинации значений переменных (минтермы) по тем или иным причинам при работе схемы никогда не встречаются. Такие комбинации, называемые избыточными, можно использовать для упрощения функций. Например, при представлении разряда десятичных цифр от 0 до 9 двоичным кодом необходимо минимум четыре разряда двоичных чисел, дающих 24 = 16 различных состояний. Из них используются десять состояний, а оставшиеся шесть функций не используются и не должны встречаться. Пусть необходимо упростить функцию , если комбинации , , являются избыточными. Нанесем на карту Карно (рис. 3.6) единицы, а крестиками пометим избыточные комбинации.   Рис. 3.6 Упрощение с использованием избыточных комбинаций: а – занесение функции избыточных комбинаций; б – доопределение функции   Если метка избыточной комбинации совпадает с единицей, то в клетку заносится крестик. Далее производиться доопределение, при котором парный крестик на карте в зависимости от удобства минимизации заменяется нулем или единицей. После доопределения функция может быть записана в виде (склеены углы карты, а также клетки нижней строки), что значительно проще исходного. 3.6. Характеристики серий логических элементов Развитие микроэлектроники привело к созданию малогабаритных, надежных и экономичных управляющих и вычислительных устройств на цифровых интегральных микросхемах (ИС). Комплект ИС, имеющих единое конструктивно-технологическое исполнение, принято называть серией. Серии ИС проектировались на основе интегральных технологий в следующей исторической последовательности:  резистивно-транзисторная логика (РТЛ);  резистивно-емкостная транзисторная логика (РЕТЛ);  диодно-транзисторная логика (ДТЛ);  транзисторно-транзисторная логика (ТТЛ);  эмиттерно-связанная логика (ЭСЛ);  транзисторно-транзисторная логика с диодами Шоттки (ТТЛШ);  интегральная инжекционная логика (И2Л);  КМОП – схемы на взаимодополняющих (комплементарных) транзисторах. В настоящее время в новых разработках применяются в основном серии ТТЛШ и КМОП, остальные серии либо сняты с производства, либо имеют ограниченное применение. В элементах транзисторно-транзисторной логикиза логический 0 принят диапазон напряжений в диапазоне 0 ÷ 0,6 В, за уровень логической 1 – 2,4 ÷ 5 В при напряжении источника питания 5 В. В свое время эти элементы получили столь широкое распространение, что для обмена сигналами между любыми цифровыми устройствами (ЭВМ, микропроцессорами и т.п.) долгое время были приняты уровни логических сигналов ТТЛ. Схема базового элемента ТТЛ представлена на рис. 3.7. 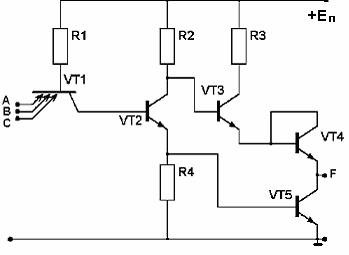Рис. 3.7 Схема элемента ТТЛ Входной каскад выполнен на многоэмиттерном транзисторе VT1, фазоразделительный – на транзисторе VT2, транзисторы VT3 и VT5 образуют выходной каскад. При поступлении сигналов низкого уровня (логических нулей) на входы А, В и С можно считать, что они находятся под потенциалом, примерно равным потенциалу общего провода (земли). Ток от источника +Еп через резистор R1 и эмиттерные переходы VT1 стечёт на землю, его коллекторный переход будет заперт, и ток базы VT2 близок к нулю. Ввиду этого VT2 заперт, и потенциал его коллектора будет высоким, а эмиттера – низким. Это приведёт к тому, что VT3 будет открыт, а VT5 – заперт. Через резистор R3, открытый VT3 и транзистор VT4, включённом как диод, от источника +Еп к выходу F поступит высокий потенциал логической единицы. Если на один или два входа подать высокий уровень логической единицы, то соответствующие эмиттерные переходы VT1 закроются под действием обратного напряжения, но через оставшийся открытым переход ток резистора R1 будет по-прежнему стекать на землю, и никаких изменений в состоянии схемы не произойдёт. Только при подаче высоких уровней на все входы А, В и С транзистора VT1 все его эмиттерные переходы закроются и ток резистора R1 от источника +Еп пойдет через переход база-коллектор VT1 в базу транзистора VT2, что приведет к его открыванию. Под действием протекающего через него тока создаются падения напряжений на R2 и R4, потенциал коллектора VT2 падает, а эмиттера – возрастает. Это ведёт к запиранию VT3 и отпиранию VT5. Через последний выход F оказывается соединённым с общим проводом и на выходе будет уровень логического нуля. Таким образом, этим элементом реализуется логическая функция 3И-НЕ: . Транзистор VT4 в диодном включении служит для более надёжного запирания VT3. Транзисторы VT3, VT4 и VT5 (см. рис. 3.7) образуют так называемый сложный инвертор. В каждом состоянии ЛЭ один из двух выходных транзисторов – VT3 или VT5 – отперт. Благодаря этому выходное сопротивление ЛЭ в обоих состояниях достаточно мало. Тем самым обеспечивается быстрый заряд и разряд паразитных емкостей, которые могут быть на выходе. Во время переключения транзисторов VT3 и VT5 из одного состояния в другое ток, потребляемый ЛЭ от источника питания, резко возрастает. Причина в том, что при переключениях оба транзистора в течение весьма короткого времени бывают отперты одновременно и ток в цепи питания ограничен только резистором R3 (около 130 Ом). КМДП – комплементарные полевые транзисторы. «Комплементарный» значит дополняющий. КМДП – основной элемент микромощной электроники. КМДП ИС – самые экономичные по расходу электроэнергии и (что особенно важно!) по тепловыделению в процессе работы. Поэтому КМДП ИС завоёвывают ведущее положение в цифровой электронике: в схемах оперативной памяти и в конструкциях процессоров как персональных компьютеров, так и больших ЭВМ. Один элемент КМДП ИС образован двумя полевыми транзисторами: один с p-каналом, другой с n-каналом (рис. 3.8).   Рис. 3.8 Инвертор на КМДП. Принципиальная схема   Пусть Vвх = +Vпит (на входе логическая 1), тогда n-канал открыт, p-канал закрыт, тогда на выходе Vвых = 0 (на выходе логический 0). Если Vвх = 0 (на входе логический 0), тогда n-канал закрыт, р-канал открыт, на выходе Vвых = Vпит (на выходе логическая 1). В любом из состояний один из транзисторов закрыт и ток потребления практически отсутствует. На рис. 3.9 приведена схема логического элемента И-НЕ, выполненного по технологии КМОП. Эта схема состоит из двух групп ключей на полевых транзисторах VT1, VT2, VT3 и VT4. Каждая группа управляется одним сигналом Вх 1 или Вх 2. При Вх 1 = = Вх 2 = 0 (низкие потенциалы) нижние n-канальные транзисторы заперты, а верхние р-канальные открыты и Вых = 1(высокий потенциал источника питания). Только при Вх 1 = Вх 2 = 1 оба нижних транзистора откроются, а оба верхних – закроются и Вых = 0.   Рис.3.9 Логический элемент 2И-Не   Применение полевых транзисторов с изолированным затвором обеспечивает высокое входное сопротивление микросхем КМОП. Благодаря малой входной емкости и высокому сопротивлению микросхемы КМОП чувствительны к статическому электричеству. Пробой изоляции под затвором происходит при напряжении около 30 В, в результате чего транзистор повреждается.

3.7. Синтез комбинационных схем

Комбинационные схемы (КС) – логические устройства, состояния выходов которых зависят только от состояния входов в данный момент времени и от предшествующего состояния не зависят.

Отличительной особенностью КС является независимость их состояния от предыстории, что в схемотехническом решении отличает их от последовательностных схем отсутствием элементов памяти. К числу комбинационных схем функционального назначения относятся: сумматоры, преобразователи кодов, шифраторы, дешифраторы, мультиплексоры, демультиплексоры и т.п.

Рис. 3.10 Синтез преобразователя кодов: а – задание преобразователя;

б – схема синтезированного преобразователя; в – таблица истинности

преобразователя кода; г – минимизация функций выхода методом карт Карно

Под комбинационными схемами понимают схемы, комбинация сигналов на выходе которой в любой момент времени однозначно определяется комбинацией сигналов на ее входе. Примером КС могут служить разнообразные шифраторы, дешифраторы, преобразователи кодов и целый ряд других схем, не содержащих элементов памяти.

Синтез КС рассмотрим на примере преобразователя кодов, представленного на рис. 3.10. Соотношение между кодовыми комбинациями на входе и выходе преобразователя задано приведенной на рис. 3.10, в.

Для минимизации функций выходов y₁, y₂, y₃ используем метод карт Карно.