Аксиомы и законы алгебры логики

Под логической аксиомой понимается формула логико-математического языка, принимаемая в качестве аксиомы при построении формальной теории, истинная в любой структуре для данного языка в силу смысла логических символов. Логические аксиомы выбираются таким образом, чтобы множество логических следствий из аксиом в точности совпадало с множеством теорем.

Алгебра логики строится на основе следующих аксиом:

1) Переменная может принимать лишь одно из двух возможных значений:

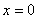, если ; 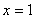, если .

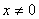2) Вводится преобразование, называемое инверсией, такое, что

; ; ; .

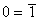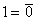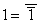3) Вводится преобразование, называемое дизъюнкцией, для которого справедливы соотношения:

; ; ; .

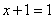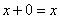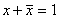4) Вводится преобразование, называемое конъюнкцией, для которого справедливы соотношения:

; ; ; .

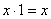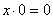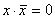5) Соотношения для штриха Шеффера:

; ; ; ; .

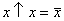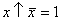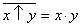6) Соотношения для стрелки Пирса:

; ; ; ; .

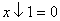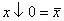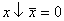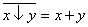Соотношения 1-6 проверяются подстановкой логических значений “0” и “1”.

На основе рассмотренных выше аксиом, выводятся теоремы, содержащие основные законы АЛ:

1) Коммутативный (переместительный) закон:

; .

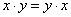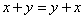2) Ассоциативный (сочетательный) закон:

; .

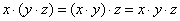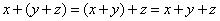3) Дистрибутивный (распределительный) закон:

; .

4) Законы поглощения:

; .

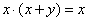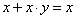5) Закон склеивания:

;

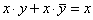6) Законы инверсии (теоремы де Моргана):

; .

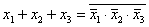Справедливость любого закона АЛ можно доказать разными методами. Проще всего это можно сделать прямой подстановки вместо переменной значений 0 и 1. Ряд законов доказывается методом перебора всех возможных значений переменных, для которых проверяется справедливость закона. Для доказательства закона достаточно показать тождественность выражений, образующих левую и правую стороны доказываемого соотношения при всех наборах переменных, принимающих значения 0 или 1.