
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Аналитическое представление булевых функций
В данном подразделе более подробно рассматривается аналитическое представление булевых функций в виде уравнений с использованием операций дизъюнкции (ИЛИ), конъюнкции (И), и отрицания (  ). Данные операции образуют, как было показано выше, булев базис.
). Данные операции образуют, как было показано выше, булев базис.
1) Аналитический способ. Рассмотрим основные понятия и определения, используемые при аналитическом представлении булевых функций.
Элементарное произведение – произведение (конъюнкция) любого числа букв (переменных) булевой функции, взятых с отрицанием или без. Например, x1∙x2∙x3;  1∙x3.
1∙x3.
Дизъюнктивная нормальная форма (ДНФ) – дизъюнкция элементарных произведений. Термин "нормальная" означает, что в данном выражении отсутствуют групповые инверсии, т.е. инверсия над несколькими переменными сразу. Пример ДНФ:
 . (3.1)
. (3.1)
Минтерм – произведение всех переменных, взятых с отрицанием или без, соответствующих двоичным наборам, на которых функция принимает значение 1. Минтерм можно назвать полной элементарной конъюнкцией. Пример: первое произведение  в выражении 3.1.
в выражении 3.1.
Ранг выражения – количество переменных, входящих в функцию или минтерм. В выражении 3.1 функция и все минтермы имеют четвёртый ранг.
Совершенной ДНФ (СДНФ) называется ДНФ, содержащая все полные элементарные конъюнкции (конституанты 1) данной булевой функции, в которой нет одинаковых элементарных конъюнкций, и каждая из них содержит все переменные данной булевой функции, причем каждую переменную – только один раз (включая вхождения с отрицанием или без отрицания). Другими словами СДНФ – это дизъюнкция всех минтермов булевой функции. Признаком того, что ДНФ является совершенной, является равенство рангов функции и всех минтермов. Функция 3.1 является СДНФ.
Элементарная сумма – логическая сумма (дизъюнкция) любого числа букв (переменных) булевой функции, взятых с отрицанием или без. Например, (x1 + x2 + x3); (  ).
).
Конъюнктивная нормальная форма (КНФ) – конъюнкция элементарных сумм. Термин "нормальная" означает, что в данном выражении отсутствуют групповые
инверсии, т.е. инверсия над несколькими переменными сразу. Пример КНФ:
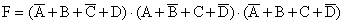 .
.
Макстерм – сумма всех переменных, взятых с отрицанием или без, соответствующих двоичным наборам, на которых функция принимает значение 0. Макстерм можно назвать полной элементарной дизъюнкцией. Пример:  .
.
Совершенной КНФ (СКНФ) называется КНФ, содержащая все полные элементарные дизъюнкции (конституанты 0) данной булевой функции, в которой нет одинаковых элементарных дизъюнкций, и каждая из них содержит все переменные данной булевой функции, причем каждую переменную – только один раз (включая вхождения с отрицанием или без отрицания). Другими словами СКНФ – это конъюнкция всех макстермов булевой функции.
В связи с тем, что одной и той же булевой функции могут соответствовать различные формы аналитической записи, то возникает задача нахождения такой формы записи, при которой каждой функции будет соответствовать одна и только одна формула стандартного типа, и каждой формуле стандартного типа будет соответствовать одна и только одна функция. Такие формы записи булевых функций называются каноническими. СДНФ и СКНФ являются каноническими формами представления булевых функций. Чаще используется ДНФ или СДНФ.
2) Табличный способ. При этом способе функция задается в виде таблицы истинности, представляющей собой совокупность всех наборов переменных и соответствующих им значений функции.

Рис. 3.2 Функциональное обозначение цифрового автомата трех переменных
Таблица истинности содержит 2m строк, m столбцов (по количеству входов) и один столбец для записи значения функции.
Например: пусть требуется задать функцию трех переменных  (рис. 3.2), т.е. автомат на три входа и на один выход, следовательно, M = 3, N = 8.
(рис. 3.2), т.е. автомат на три входа и на один выход, следовательно, M = 3, N = 8.
Следующий способ задания дискретного автомата – числовой. В Этом случае функция задается в виде десятичных эквивалентов номеров наборов аргументов, при которых функция принимает единичное значение. Например, для рассмотренного выше примера функция F1 принимает единичные значения на наборах переменных со следующими номерами: 1, 2, 5, тогда числовой способ задания будет иметь вид  (табл. 3.4).
(табл. 3.4).
Таблица 3.4
Таблица состояний цифрового автомата трех переменных
| Номер | 
| 
| 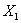
| 
|
Дата добавления: 2015-04-16; просмотров: 315; Мы поможем в написании вашей работы!; Нарушение авторских прав |