Задача 1. Решение задачи 1 требует знания основных законов постоянного тока, производных формул этих законов и умения их применять для расчета электрических цепей со

Решение задачи 1 требует знания основных законов постоянного тока, производных формул этих законов и умения их применять для расчета электрических цепей со смешанным соединением резисторов.

Методику и последовательность действий при решении задач со смешанным соединением резисторов рассмотрим в общем виде на конкретном примере.

1 Выписываем условие задачи (содержание условий задач выписывать применительно к своему варианту).

Условие задачи: цепь постоянного тока со смешанным соединением состоит из четырех резисторов. Заданы схема цепи (рисунок 1), значения сопротивлений резисторов: R₁ = 30Ом, R₂ = 20Ом, R₃ = 3Ом, R₄ = 5Ом, мощность цепи Р = 320Вт.

Определить: эквивалентное сопротивление цепи R_эк; токи, проходящие через каждый резистор. Решение задачи проверить, применив первый закон Кирхгофа.

2 Выписываем из условий то, что дано и нужно определять в виде буквенных обозначений и числовых значений.

3 Продумаем порядок решения, подбирая при необходимости справочный материал. В нашем случае принимаем такой порядок решения:

1) находим эквивалентное сопротивление цепи:

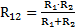(1)

2) обозначим токи I₁, I₂, I₃, I₄ на рис.1 стрелками и определим их значения из формулы мощности:

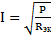(2)

Расчетные значения параметров цепи можно определить по следующим формулам:

I₂ = I₄ = I, (3)

I₁ = U₁₂/R, (4)

I₂ = U₁₂/R₂, (5)

U₁₂ = IR₁₂. (6)

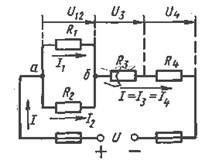
Рисунок 1 – Схема цепи к примеру 1

4 Выполняем решение, не забывая нумеровать и кратко описывать действия. Именно так решены все типовые примеры пособия. Отсутствие письменных пояснений действий приводит к неполному пониманию решения задач, быстро забываются.

5 Выполняем проверку решения следующими способами: логичность получения такого результата; проверка результатов с применением первого и второго закона Кирхгофа, подсчетом баланса мощности; сравнивание результатов решением задачи другими способами.

Объясним некоторые способы проверки результатов решения.

Применение первого закона Кирхгофа. Формулировка закона: алгебраическая сумма токов в узловой точке равна нулю. Математическая запись для узла б схемы цепи рис.1:

I₁+I₂−I = 0. (7)

Применение второго закона Кирхгофа. Формулировка закона:во всяком замкнутом контуре электрической цепи алгебраическая сумма электродвижущих сил равна алгебраической сумме падений напряжений на отдельных сопротивлениях этого контура.

В замкнутом контуре (рис.1) приложенное напряжение U (аналогично ЭДС при внутреннем сопротивлении источника тока, равном нулю) и падения напряжения:

U₁₂ = IR₁₂, (8)

U₃ = IR₃, (9)

U₄ = IR₄. (10)

Обходя контур по направлению тока (в данном случае по часовой стрелке), составим уравнение по второму закону Кирхгофа:

U = U₁₂+U₃+U₄ (11)

Подсчет баланса мощности. Общая мощность цепи равна сумме мощностей на отдельных резисторах. Для схемы цепи (рис.1):

Р = Р₁+Р₂+Р₃+Р₄; (12)

так как Р = I²R или Р=U²/R, то

Р = I₁²R₁+I₂²R₂+I₃²R₃+I₄²R₄ (12а)

или

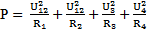(12б)

Если проверку решения проводить путем сравнения результатов решения другими способами, то в данном случае вместо определения тока из формулы:

P = I²R_эк (13)

можно было найти напряжение, а затем ток по формуле закона Ома.