
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача 1. Задача 1 предусматривает расчет трехфазной цепи переменного тока при соединении приемников электрической энергии в звезду или треугольник
Задача 1 предусматривает расчет трехфазной цепи переменного тока при соединении приемников электрической энергии в звезду или треугольник. Для успешного решения задачи необходимо разобраться в заданной схеме соединений и в соотношениях линейных и фазных токов и напряжений для этой схемы, воспользовавшись следующим алгоритмом:
1. Определить полное сопротивление каждой фазы приемника энергии (потребителя)
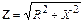 (18)
(18)
2. Определить фазное напряжение Uф в зависимости от схемы соединения, для треугольника и звезды соответственно

 , (19)
, (19) 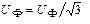 (20)
(20)
3. Определить токи в каждой фазе потребителя

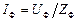 (21)
(21)
4. Определить линейные токи Iа, Ib, и Ic в зависимости от схемы соединения: для звезды Iл = Iф; для треугольника проще всего найти токи Iл графически из векторной диаграммы. Величина тока определяется умножением длины соответствующего вектора на масштаб тока. Кроме того, величину этих токов можно определить аналитически.
5. При соединении треугольником напряжения Uф = Uл, поэтому построение векторной диаграммы начинаем с построения в выбранном масштабе векторов напряжений. Ниже вектора обозначаются выделение жирным шрифтом или черточкой сверху буквы.
Угол сдвига по фазе между Uф и Iф зависит от характера нагрузки. При активной нагрузке - Uф и Iф совпадают по фазе, при активно-индуктивной нагрузке - Iф отстает от Uф на угол j, при активно-емкостной - Iф опережает Uф на угол j. Значение этого угла можно найти из треугольника сопротивлений (рисунок 7) по расчетным формулам
j = arctg(X/R), (22а)
j = arccos(R/Z). (22б)

Рисунок 7 – Треугольник сопротивлений
Определив угол в каждой фазе потребителя по формулам (22а,б), строим векторы фазных токов Iф. Затем согласно векторным уравнениям:
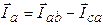 , (23а)
, (23а)
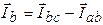 , (23б)
, (23б)
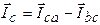 . (23в)
. (23в)
Строим векторы линейных токов и определяем их величины
I = L∙M (24)
где L - длина вектора в мм;
M - масштаб [А/мм].
2 При соединении звездой с нейтральным проводом фазные напряжения Uф равны между собой и определяются
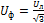 (25)
(25)
Построение векторной диаграммы начинаем с построения в выбранном масштабе векторов фазных напряжений Ua, Ub и Uc. Векторы линейных напряжений строим по уравнениям:
 , (26а)
, (26а)
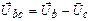 , (26б)
, (26б)
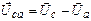 . (26в)
. (26в)
Векторы токов Iф = Iл строим в зависимости от углов их сдвига по фазе относительно соответствующих фазных напряжений.
Наконец, строим вектор тока нейтрального провода как геометрическую сумму векторов фазных токов
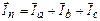 (27)
(27)
Рассмотрим пример:
Пусть задана схема на рисунке 8 и ее параметры:
Uл = 36В; Х = 5,2Ом; R = 9Ом.
Напряжения фаз источника и нагрузки Uф одинаковы (ведь сопротивлением проводов мы пренебрегаем), тогда согласно формуле (26) получим 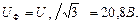
Для звезды линейные токи равны токам фаз, а значит по закону Ома:
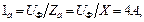


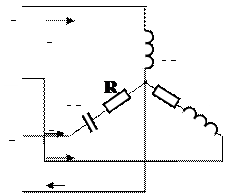 |
Рисунок 8 – Схема для примера решения задачи
Построение векторной диаграммы (рисунок 9) начинаем с построения в выбранном масштабе векторов линейных и фазных напряжений.
Векторы токов строим в выбранном масштабе токов, учитывая углы сдвига по фазе (рис.9).
В активно-индуктивной нагрузке ток по фазе отстает от напряжения, а в активно-емкостной нагрузке опережает его на некоторый угол j .
Для схемы рассматриваемого примера j = 900, j = 300, j = -300 согласно схеме цепи (рис.8).
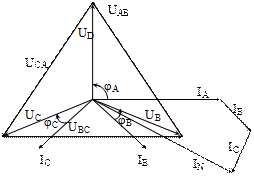 |
На основании первого закона Кирхгофа (16) для узла «0» ток нейтрального провода IN равен геометрической сумме токов фаз Ia , Ib и Ic.
Рисунок 9 – Векторная диаграмма
Дата добавления: 2015-04-16; просмотров: 328; Мы поможем в написании вашей работы!; Нарушение авторских прав |