Энтальпия образования химических соединений.

Энтальпией (теплотой) образования химического соединения DН_Т называется изменение энтальпии в процессе получения одного моля этого соедине­ния из простых веществ, устойчивых при данной температуре.

Стандартной энтальпией (теплотой) обра­зования химического соединения DН , _обр называют изменение энтальпии в процессе образования одного моля этого соединения, находящегося в стандартном состоянии (Т = 298 К и r = 101,3 кПа), из простых веществ, также находящихся в стандартных состояниях и термодинами­чески устойчивых при данной температуре фазах и модифика­циях (таблица А.1).

Стандартные энтальпии образования простых веществ прини­маются равными нулю, если их агрегатные состояния и модифи­кации устойчивы при стандартных условиях. Так, например, нулю равны стандартная теплота образования жидкого брома (а не газообразного) и графита (а не алмаза).

Стандартная энтальпия образования соединения – мера его термодинамической устойчивости, прочности, количественное выраже­ние энергетических свойств соеди­нения.

Термохимические расчеты.В основе большинства термохими­ческих расчетов лежит следствие из закона Гесса: тепловой эф­фект химической реакции равен сумме теплот (энтальпий) обра­зования продуктов реакции за вычетом суммы теплот (энталь­пий) образования исходных веществ с учетом их стехиометрических коэффициентов в уравнении реакции.

DН_х.р. = S DН_обр. (прод. р-ции) - S DН_обр (исх. в-в.) (9)

Уравнение (9) позволяет определять как тепловой эффект реакции по известным энтальпиям образования веществ, участву­ющих в реакции, так и одну из энтальпий образования, если известны тепловой эффект реакции и все остальные энтальпии образования.

Тепловой эффект химической реакции является энергетиче­ским эффектом процесса, протекающего при постоянной темпера­туре. Пользуясь справочными данными, которые относятся к 298 К, можно рассчитать тепловые эффекты реакций, протекаю­щих при этой температуре. Однако при выполнении термохимических расчетов, допуская обычно незначительную ошиб­ку, можно пользоваться стандартными значениями теплот обра­зования даже тогда, когда условия протекания процесса отлича­ются от стандартных.

Тепловые эффекты фазовых превращений.Фазовые превра­щения часто сопутствуют химическим реакциям. Однако тепло­вые эффекты фазовых превращений, как правило, меньше тепло­вых эффектов химических реакций. Ниже приведены примеры термохимических уравнений некоторых фазовых превращений:

Н₂О_(ж) ® Н₂О_(г), DH = 44,0 кДж/моль,

Н₂О_(к) ® Н₂О_(ж), DH = 6,0 кДж/моль,

I_2(к) ® I_2(г), DH = 62,24 кДж/моль.

Исходя из выше приведенных данных можно отметить, что фазовый переход из более в менее конденсированное состояние ведет к повышению энтальпии системы (тепло поглощается – процесс эндотермический).

Т Ж Г

Переход вещества из аморфного состояния в кристаллическое всегда сопровождается выделением теплоты (DH <0) – процесс экзотермический:

Sb_(аморф) ® Sb_(к), DH = -10,62 кДж/моль,

В₂О_{3(аморф.)} ® В₂О_3(к), DH = -25,08 кДж/моль.

Самопроизвольные и несамопроизвольные процессы.Многие процессы осуществляются самопроизвольно, т. е. без затраты работы извне. В результате их может быть получена работа против внешних сил, пропорциональная происшедшему изменению энергии системы. Так, самопроизвольно вода стекает по на­клонному желобу или теплота передается от более нагретого тела к менее нагретому. В ходе самопро­извольного процесса система теряет способность производить полезную работу.

Самопроизвольный процесс не может протекать в обратном направлении так же самопроизвольно, как в прямом. Так, вода не может сама по себе перетекать вверх по наклонному желобу, а теплота не может сама по себе переходить от холодного тела к горячему. Чтобы перекачать воду наверх или передать теплоту от холодной части системы к горячей, необходимо совершить работу над системой. К процессам, обратным по отношению к самопроизвольным, применяется термин «несамопроизвольные».

При изучении химических взаимодействий очень важно оце­нить возможность или невозможность их самопроизвольного протекания при заданных условиях, выяснить химическое срод­ство веществ. Должен быть критерий, с помощью которого можно было бы установить принципиальную осуществимость, направление и пределы самопроизвольного течения реакции при тех или иных температурах и давлениях. Первый закон термоди­намики такого критерия не дает. Тепловой эффект реакции не определяет направления процесса: самопроизвольно могут проте­кать как экзотермические, так и эндотермические реакции.

Критерий самопроизвольного протекания процесса в изолиро­ванных системах дает второй закон термодинамики. Прежде чем перейти к рассмотрению этого закона, введем представление о термодинамической функции состояния системы, называемой энтропией.

Энтропия.Для характеристики состояния некоторого количе­ства вещества, являющегося совокупностью очень большого чи­сла молекул, можно или указать температуру, давление и другие термодинамические параметры состояния системы, или указать мгновенные координаты каждой молекулы (x_i, y_i, z_i) и скорости перемещения по всем трем направлениям (v_xi,v_yi,v_zi). В первом случае охарактеризовывается макросостояние системы, во вто­ром – микросостояние. Каждому макросостоянию отвечает огромное число микросостояний. Число микросостояний, с помощью которых осуществляется данное макросостояние, называют тер­модинамической вероятностью состояния системы и обознача­ют W.

Термодинамическая вероятность состояния системы, состоя­щей всего из 10 молекул газа, примерно 1000, а ведь только в 1 см³ газа содержится 2,7×10¹⁹ молекул (н. у.). Чтобы перейти к более удобным для восприятия и расчетов числам, в термодина­мике используют не величину W, а ее логарифм lnW. Последнему можно придать размерность (Дж/К), умножив на константу Больцмана k:

klnW = S. (10)

Величину S называют энтропией системы.

Энтропия – термодинамическая функция состояния си­стемы и ее величина зависит от количества рассматриваемого вещества. Поэтому целесообразно относить величину энтропии к одному молю вещества (Дж/(моль×К)) и выражать как

RlnW = S. (11)

где R = kN_A – молярная газовая постоянная;

N_A – постоянная Авогадро.

Из уравнения (11) следует, что энтропия системы увели­чивается пропорционально логарифму термодинамической веро­ятности состояния W. Это соотношение лежит в основе современ­ной статистической термодинамики.

При р = const энтропия является функцией температуры Т, причем температура замерзания и тем­пература кипения – это те точки, в которых энтропия из­меняется особенно резко, скачкообразно.

Итак, энтропия S является мерой неупорядоченности системы. «Носителями» энтропии являются газы. Если при реакции увеличивается число молей газообразных веществ, то увеличивается и энтропия. Т.е. не производя расчетов можно при необходимости определить знак изменения энтропии системы:

C_(к) + О_2(г) = СО_2(г), DS » 0;

2C_(к) + О_2(г) = 2СО_(г), DS > 0;

N_2(г) + 3H_2(г) = 2NH_3(г), DS < 0.

В таблице А.1 приведены значения S некоторых веществ (обратите внимание на то, что известны абсолютные значения энтропии веществ, в то время как абсолютные значения функции U и H не известны).

Т.к. энтропия есть функция состояния системы, то изменение энтропии (DS) при химической реакции равно сумме энтропий продуктов реакции за вычетом суммы энтропий исходных веществ с учетом их стехиометрических коэффициентов в уравнении реакции.

DS_х.р. = S S_обр. (прод. р-ции) - S S_обр (исх. в-в.) (12)

Направление и предел протекания процессов в изолированных системах. Второй закон термодинамики.Изолированные системы не обмениваются с внешней средой ни теплотой, ни работой. На основании уравнения (9) можно утверждать, что при q = 0 и A = 0 величина DU тоже равна нулю, т. е. внутренняя энергия изолированной системы постоянна (U=const); постоя­нен и ее объем (V = const). В изолированных системах само­произвольно идут только те процессы, которые сопровождаются ростом энтропии системы: DS>0; при этом преде­лом самопроизвольного течения процесса является достижение максимальной для данных условий энтропии S^max.

Рассмотренное положение представляет одну из формулиро­вок второго закона термодинамики (закон имеет статистический характер, т. е. применим лишь к системам, состоящим из очень большого числа частиц). Требование постоянства внутренней энергии и объема системы исключает использование энтропии как критерия направления и предела протекания химических реакций, при которых внутренняя энергия веществ неизбежно меняется, а также совершается работа расширения против вне­шнего давления.

Энтропийный и энтальпийный факторы химических реакций, протекающих в изобарно-изотермических условиях.Движущей силой процесса, протекающего в изобарно-изотермических усло­виях, может быть или стремление системы перейти в состояние с наименьшей энергией, т. е. выделить теплоту в окружающую среду, уменьшить энтальпию (DH<0), или стремление системы перейти в состояние с наибольшей термодинамической вероят­ностью, т. е. увеличить энтропию (DS>0). Если процесс протекает так, что DH=0, то рост энтропии становится его единственной движущей силой. И, наоборот, при условии DS = 0 единственной движущей силой процесса является убыль энтальпии. В связи с этим можно говорить об энтальпийном DH и энтропийном TDS факторах процесса.

Максимальная работа.Голландский физико-химик Вант-Гофф предложил новую теорию химического сродства, которая, не объясняя природы химического сродства, ограничивается ука­занием способа его измерения, т. е. дает количественную оценку химическому сродству.

Вант-Гофф использует в качестве меры химического сродства максимальную работу 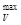А или А для реакций, протекающих при V, T = const или р, Т = const соответственно.

Максимальная работа равна энергии, которую нужно прило­жить к системе, чтобы остановить реакцию, т. е. преодолеть, силы химического сродства. Поскольку реакция протекает в направле­нии совершения положительной максимальной работы, знак 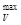А или А определяет направление самопроизвольного тече­ния химического взаимодействия.

Максимальная работа при постоянном объеме равна

А 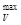= -DU + TDS (13)

или

А 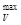= -(U₂ – U₁) + T(S₂ – S₁) = -[(U₂ – TS₂) – (U₁ – TS₁)] (14)

где U₁, S₁ и U₂, S₂ – величина внутренней энергии и энтропии системы в исходном и конечном состояниях соответственно.

Разность (U - TS) называют энергией Гельмгольца системы и обозначают буквой F. Таким образом,

А 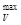= -DF. (15)