
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ПОКАЗАТЕЛЬНАЯ ФОРМА КОМПЛЕКСНОГО ЧИСЛА
Рассмотрим некоторые свойства экспоненциальной функции
f (x) = eах.
Пусть f(x  ) = еax
) = еax  и f(x2) = еах
и f(x2) = еах 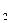 .
.
Тогда
f(x  ) f(x
) f(x 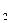 ) = eax
) = eax  ·еах
·еах 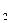 = e
= e  . (33)
. (33)
Известно, что
(еах)´ = а·еах, (34)
т. е. экспоненциальная функция обладает следующими двумя свойствами:
f(x  )·f(x
)·f(x 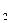 ) = f(x
) = f(x  + x
+ x  ), (35)
), (35)
f´(x) = а·еах = a·f x).
Теперь рассмотрим функцию:
 (φ) = cos φ + i sin φ (36)
(φ) = cos φ + i sin φ (36)
Убедимся, что она обладает теми же свойствами:
(cos φ  + i sin φ
+ i sin φ  ) (cos φ 2 + i sin φ 2) =
) (cos φ 2 + i sin φ 2) =
= cos φ  · cos φ 2 + cos φ
· cos φ 2 + cos φ  · i sin φ 2 + i sin φ
· i sin φ 2 + i sin φ  ·cos φ 2 + i sin φ
·cos φ 2 + i sin φ  · i sin φ 2 =
· i sin φ 2 =
= cos(φ  + φ 2) + i sin(φ
+ φ 2) + i sin(φ  + φ 2). (37)
+ φ 2). (37)
(cos φ + i sin φ)´ = – sin φ + i cos φ =
=  sin φ + icos φ = i (cos φ + i sin φ). (38)
sin φ + icos φ = i (cos φ + i sin φ). (38)
Полагая а = i, можем считать, что функции eiφ и  (φ) ведут себя одинаково, т. е. можно считать:
(φ) ведут себя одинаково, т. е. можно считать:
eiφ = cos φ + i sin φ (39)
Это равенство называется формулой Эйлера[14].
Пользуясь формулой Эйлера, можно представить комплексное число
в тригонометрической форме
Z = а + i b = |Z| (cos φ + i sin φ)
и в показательной форме:
Z = |Z| ei argZ = ρeiφ (40)
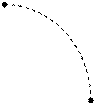
Чтобы по выражению (40) найти на комплексной плоскости точку, соответствующую числу Z, достаточно отложить от начала координат на действительной оси отрезок величиной |Z| и повернуть его вокруг центра координат на угол φ в положительном направлении (рис.9)

| |

 Y
Y
|
 0 X
0 X
| | |||
| | |||
|Z|
Рис. 9
Поэтому множитель eiφ иногда называют оператором поворота.
В частности,
1 = е  ; i = е
; i = е  ; – 1 = e
; – 1 = e  ; – i = e
; – i = e 
Аргумент комплексного числа является естественным обобщением знака действительного числа. В самом деле, аргументы положительных и отрицательных чисел равны соответственно 0 и p.
Рассмотрим примеры умножения и деления комплексных чисел в показательной форме.
Пример 1.
(7e 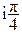 )(0,5e
)(0,5e 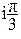 ) = 7· 0,5
) = 7· 0,5  = 3,5
= 3,5 
Здесь сразу видны полярные координаты (3,5; 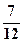 p) результата перемно-жения.
p) результата перемно-жения.
Пример 2.
(6e  ) : (2e
) : (2e  ) =
) =  e
e  = 3e
= 3e  .
.
Дата добавления: 2014-11-13; просмотров: 407; Мы поможем в написании вашей работы!; Нарушение авторских прав |