ПОНЯТИЕ КОМПЛЕКСНОГО ЧИСЛА

История математики показывает, что введение различных обратных действий над числами всякий раз приводило к расширению понятия числа. Так, введение действия, обратного сложению, т. е. вычитания, привело к появлению отрицательных чисел, и понятие числа стало связываться с системой целых чисел, состоящих из всех положительных чисел, нуля (его обозначение было введено значительно позднее) и всех отрицательных чисел. Деление, как действие, обратное умножению, привело к построению более широкой системы – системы рациональных чисел, состоящей из всех дробных чисел, как положительных, так и отрицательных. Употребление действия, обратного возведению в степень, т. е. извлечение корня, привело к расширению понятия о числе уже до масштабов системы действительных (или вещественных)[7] чисел.

Становление теории действительных чисел относится ко второй половине XIX века. Однако уже задолго до этого был поставлен вопрос о необходимости дальнейшего расширения числовой системы. Эта потребность появилась с построением теории решения квадратных уравнений. Например, простейшее из квадратных уравнений вида

х² + 1 = 0 (2)

не имеет корней на множестве действительных чисел. Это и заставило ещё в XVI веке изучать квадратные корни из отрицательных чисел. Ввиду того, что получающийся при этом результат в ту пору не мог быть истолкован как итог какого-либо непосредственного счёта или измерения, такие числа стали называться «мнимыми».

Обозначим = i (или i² = –1) (3)

Тогда ,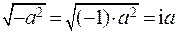

где а – любое действительное число.

Выражение i = (4) называется мнимой единицей.

Когда при решении полного квадратного уравнения

Ах ² + Bx + С = О (5)

по хорошо известной формуле

(6)

выражение под корнем – дискриминант[8] – оказывается отрицательным, то решение принимает форму а + ib, где а и b выражаются действительными числами. Здесь величину первого слагаемого а можно считать действи-тельной частью решения, а величину второго слагаемого b - мнимой. В частных случаях корни могут быть чисто действительными (когда дискриминант больше нуля или равен нулю) и чисто мнимыми (когда в вышеприведенном квадратном уравнении коэффициенты A и С имеют одинаковые знаки, а В =0). Числа, состоящие из действительной и мнимой частей, называются комплексными[9] и обозначаются:

Z = а + ib. (7)

Впервые действительные и мнимые корни были противопоставлены у Рене Декарта[10] (1637 г.), и с тех пор для действительной а и мнимой b

составляющих комплексного числа Z = a + i b употребляются обозначения[11]

a = Re Z, (8)

b = Im Z. (9)

Комплексные числа входили в употребление, сопровождаясь большими спорами среди математиков, и были полностью «приняты на вооружение» только лишь к началу XIX века.

Расширение числовой системы присоединением к ней комплексных чисел принесло огромную пользу. Но самым выдающимся эффектом от использования аппарата комплексных чисел явилось то, что, введённые для решения квадратных уравнений, они сделали теоретически разрешимыми вообще все алгебраические уравнения. Этот факт известен как основная теорема алгебры[12].

Комплексные числа находят очень широкое применение в решении самых разнообразных практических задач.