ДОКАЗАТЕЛЬСТВО ФОРМУЛЫ ЭЙЛЕРА С ПОМОЩЬЮ СТЕПЕННЫХ РЯДОВ

Функции e^x, sin x и cos x непрерывны и дифференцируемы сколько угодно раз. Для представления каждой из них степенным рядом в окрест-

ноcти точки x = 0 (т. е. в начале координат) может быть использована

формула Маклорена[15]:

, (41)

где , n – порядок производной и х – действительное число.

(42)

(43)

(44)

Заменим x на ix в выражениях (39) и (41) с учётом:

(45)

для любого n = 0; 1; 2; 3; 4; …

(46)

Из сравнения правых частей выражений (43), (44) и (47) видно:

(47)

§ 7. ДОКАЗАТЕЛЬСТВО ФОРМУЛЫ ЭЙЛЕРА РЕШЕНИЕМ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ

Рассмотрим функцию

(48)

Продифференцируем обе части этого равенства, считая i постоянной величиной. Тогда получаем:

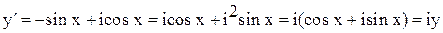
Соотношение соответствует дифференциальному уравнению первого порядка с разделяющимися переменными

(49)

Разделяя переменные, получим:

(50)

Проинтегрируем обе части этого равенства:

(51)

и получаем:

(52),

где А–произвольная постоянная величина.

или

Отсюда, потенцируя

или (53)

Из соотношения (48) при x = 0 имеем y = 1. Подставляя это в (53) для определения значения постоянной С, получаем:

Таким образом, ,

т. е. (54).

§ 8. КРАТКАЯ ИСТОРИЧЕСКАЯ СПРАВКА*

Древнегреческие математики считали «настоящими» только натуральные числа. Постепенно складывалось представление о бесконечности множества натуральных чисел. В III веке до н. э. Архимед[16] разработал систему их обозначений вплоть до такого громадного числа, как

Наряду с натуральными числами древние ассирийцы, египтяне и греки применяли дроби, т. е. числа, составленные из целого числа долей единицы[17]. Долгое время полагали, что результат измерения всегда выражается либо в виде натурального числа, либо в виде отношения таких чисел.

Пифагор[18] учил, что «… числа являются элементами всех вещей, и

весь мир в целом является гармонией и числом». Сильнейший удар по этому взгляду был нанесён открытием, сделанным одним из пифагорейцев, который доказал, что диагональ квадрата несоизмерима с его стороной. Отсюда следует, что натуральных чисел и дробей недостаточно для того, чтобы выразить длину диагонали квадрата со стороной 1. Есть основание утверждать, что именно с этого открытия и начинается эра теоретической математики, т. к. открыть существование несоизмеримых величин с помощью опыта, не прибегая к абстрактному рассуждению, было невозможно.

Следующим важным этапом в развитии понятия о числе было введение отрицательных чисел. Это было сделано китайскими математиками за два века до н. э. Отрицательные числа применял в III веке (н. э.) и Диофант[19], знавший уже правила действия над ними, а в VII веке эти числа уже подробно изучили индийские учёные, которые сравнивали такие числа с долгом. С помощью отрицательных чисел можно было единым образом описывать изменения величин. Уже в VIII веке было установлено, что квадратный корень из положительного числа имеет два значения – положительное и отрицательное, но при этом считалось, что из отрицательных чисел извлекать квадратный корень нельзя, т. к., якобы, нет такого числа х, чтобы x² = – 9.

В XVI же веке в связи с изучением кубических уравнений оказалось необходимым извлекать квадратные корни из отрицательных чисел. В формуле для решения кубических уравнений вида 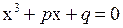фигурируют кубические и квадратные корни:

.

Эта формула безотказно действовала в случаях, когда уравнение имело один действительный корень (например, ), а если уравнение имело три действительных корня (например, ), то под знаком квадратного корня оказывалось отрицательное число. Получалось, что путь к этим корням ведёт через недопустимую по тем временам операцию извлечения квадратного корня из отрицательного числа.

Вслед за тем, как были решены уравнения 4-й степени, математики усиленно искали формулу для решения уравнения 5-й степени. Но Руффини[20] на рубеже XVIII и XIX веков доказал, что буквенное уравнение пятой степени

нельзя решить алгебраически, точнее, нельзя выразить его корень через буквенные величины a, b, c, d, e с помощью шести алгебраических действий (сложения, вычитания, умножения, деления, возведения в степень и извлечения корня).

В 1824 году Абель[21] доказал, что никакое общее уравнение, степень которого больше 4-х, нельзя решить в радикалах. Тем не менее, всякое уравнение n-й степени имеет (если рассматривать и комплексные числа) n корней (среди которых могут быть и равные). В этом математики были убеждены ещё в XVII веке (основываясь на разборе многочисленных частных случаев), но лишь на рубеже XVIII и XIX веков это предположение было доказано Гауссом[22].

В 1545 году Кардано[23] предложил ввести числа новой природы. Он показал, что система уравнений

,

не имеющая решений на множестве действительных чисел, имеет решение вида 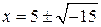, , если только условиться действовать над такими выражениями по правилам обычной алгебры и считать, что . Кардано называл такие величины «чисто отрицательными» и даже «софистически отрицательными», считал их бесполезными и старался их не употреблять. В самом деле, с помощью таких чисел нельзя выразить ни результат измерения какой-нибудь величины, ни изменение какой-нибудь величины. Но уже в 1572 году вышла книга Бомбелли[24], в которой впервые были установлены правила арифметических операций над такими числами, вплоть до извлечения из них кубических корней. Название «мнимые числа» ввёл в 1637 году Декарт, а в 1777 году Эйлер предложил использовать первую букву латинского слова imaginarius (латинское imaginarius – ‘мнимый, кажущийся, призрачный, воображаемый’) для обозначения числа (т. е. мнимой единицы). Этот символ благодаря Гауссу вошёл во всеобщее употребление. Термин «комплексные числа» так же был введён Гауссом

(в 1831 году).

В течение XVII века продолжалось обсуждение арифметической природы мнимых чисел, и делались попытки дать им геометрическое обоснование. Постепенно развивалась техника операций над мнимыми числами. Наконец, на рубеже XVII и XVIII веков была построена общая теория корней n-ых степеней (сначала из отрицательных чисел, а за тем и из любых комплексных чисел), основанная на формуле Муавра

.

Эта формула была получена Муавром в 1707 году. С её помощью легко выводятся соотношения для косинусов и синусов кратных дуг. Это было продемонстрировано в § 3.

В 1748 году Эйлер вывел замечательную формулу

,

которая связывает воедино показательную функцию с тригонометрической.

Можно считать, что с этого момента тригонометрия и алгебра стали единым

разделом математики.

С помощью формулы Эйлера стало возможным возводить число e в любую комплексную степень. Любопытно, например, что . [25]

Если прологарифмировать обе части этого равенства по основанию e, то можно обнаружить существование логарифмов от отрицательных чисел. И это не меньшая неожиданность для непосвящённого, чем возможность разложить на множители сумму квадратов двух чисел.

В тригонометрической форме комплексные числа впервые появились у Леонарда Эйлера и д’Аламбера[26]. Далее оказалось возможным находить синусы и косинусы комплексных чисел, вычислять логарифмы таких чисел, т. е. строить теорию функций комплексного переменного. И уже в конце XVIII века Лагранж[27] смог сказать, что мнимые величины теперь не затрудняют математический анализ. С помощью мнимых чисел математики научились представлять решения линейных дифференциальных уравнений с постоянными коэффициентами. (Такие уравнения встречаются, например, в теории колебаний материальной точки в сопротивляющейся среде). А Якоб Бернулли[28] начал применять комплексные числа для вычисления интегралов.

Хотя в течение XVIII века с помощью комплексных чисел были решены многие вопросы (в том числе и прикладные задачи, связанные с картографией, гидродинамикой и т. д.), однако ещё не было строгого логического обоснования теории этих чисел. Поэтому Лаплас[29] считал, что «результаты, полученные с помощью мнимых чисел, – только наведение, приобретающее характер настоящих истин лишь после подтверждения прямыми доказательствами». Карно[30] писал: «Никто ведь не сомневается в точности результатов, получаемых при вычислениях с мнимыми количествами, хотя они представляют собой только алгебраические формы-иероглифы нелепых количеств».

Наконец в конце XVIII века – начале XIX века было получено геометрическое истолкование комплексных чисел. Вессель[31], Арган[32] и Гаусс независимо друг от друга предложили изображать комплексное число 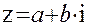точкой на координатной плоскости. Позднее оказалось, что ещё удобнее изображать число не самой точкой M, а вектором , идущим в эту точку из начала координат (т. е. радиусом-вектором точки). При таком истолковании сложению и вычитанию комплексных чисел соответствуют эти же операции над векторами. Вектор можно задавать не только его координатами a и b, но так же длиной ρ и углом φ, который он образует с положительным направлением оси абсцисс. При этом, как уже указывалось ранее, , , и число z принимает вид тригонометрической формы комплексного числа , где ρ – модуль, т. е. , а φ – аргумент, обозначаемый как аrg Z.

Термин «модуль» для комплексного числа впервые начали употреблять швейцарский математик Арган (1814 г.) и французский математик Коши[33] (1821г.). Термин «абсолютная величина» и обозначение Z ввёл Вейерштрасс[34] (1841г.). Название «аргумент» для угла φ впервые употребил Коши (1747 г.). Он же впервые употребил и название «сопряженные числа» (1831г.). Упомянутая ранее формула Эйлера, позволяет записать число Z в виде показательной формы , которая наглядно увязывается с геометрической и векторной формами. Геометрическое истолкование комплексных чисел позволило определить многие понятия, связанные с функцией комплексного переменного, значительно расширило область их применения.

Вскоре стало ясно, что комплексные числа полезны во многих вопросах, где исследователи имеют дело с векторными величинами (в том числе в задачах аэро- и гидродинамики, теории упругости, электротехники и т. д.).

После создания теории комплексных чисел возник вопрос о существовании «гиперкомплексных» чисел – чисел с несколькими «мнимыми» единицами. Такую систему вида , где , построил в 1843 году Гамильтон[35], который назвал их «кватернионами»[36]. Правила действия над кватернионами напоминают правила обычной алгебры, однако их умножение не обладает свойством коммутативности (т. е. переместительности): например, , а .[37]

Большой вклад в развитие теории функций комплексного переменного внесли русские и советские учёные. В частности, Николай Иванович Мусхелишвили (1891 – 1976), занимавшийся её применением к решению задач теории упругости, Мстислав Всеволодович Келдыш (1911 – 1978) и Михаил Алексеевич Лаврентьев (1900 – 1980), занимавшиеся приложениями этой теории к аэро– и гидродинамике, а Николай Николаевич Боголюбов (1909 – 1992) и Василий Сергеевич Владимиров (род. в 1923 году) занимались применением теории функций комплексной переменной к проблемам математической физики и квантовой теории поля.

Факт участия большого количества учёных различных националь-ностей в разработке теории комплексных чисел является одним из примеров эффективного интернационального сотрудничества, служащего интересам всего человечества в целом.

§ 9. КОНТРОЛЬНЫЕ ВОПРОСЫ К ТЕМЕ «КОМПЛЕКСНЫЕ ЧИСЛА»

1) Понятие комплексного числа. Алгебраическая форма записи комплекс--ных чисел.

2) Сложение, вычитание, умножение и деление комплексных чисел в алгебраической форме. Умножение комплексного числа на константу.

3) Геометрическая трактовка комплексных чисел. Модуль комплексного числа.

4) Умножение на постоянное число, сложение и вычитание комплексных чисел в геометрической форме.

5) Сопряжённые комплексные числа. Их сумма, разность и произведение.

6) Тригонометрическая форма комплексного числа.

7) Умножение, деление, возведение в степень и извлечение корня на комплексной плоскости в тригонометрической форме.

8) Формула Муавра и её использование для вычисления синусов и косинусов кратных дуг.

9) Показательная форма комплексного числа. Формула Эйлера.

10) Умножение, деление, возведение в степень и извлечение корня для комплексных чисел в показательной форме.

ЛИТЕРАТУРА

1. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся втузов. ― М.: Наука, Физматлит, 1998 и последующие издания.

2. Бэлл Э.Т. Творцы математики: Предшественники современной матема-тики./ Пер. с англ. – М.: Просвещение, 1979.

3. Бурбаки Н. Очерки по истории математики \ Пер. с франц. – М.: Издательство иностранной литературы, 1963.

4. Клейн Ф. Лекции о развитии математики в XIX столетии: В 2-х томах. Т.1 / Пер. с нем. – М.: «Наука», 1989.

5. Колягин Ю.М. Алгебра и начала анализа. 11 кл.: Учебник для обще-образовательных учреждений – М.: Мнемозина, 2004.

6. Математический энциклопедический словарь./ Гл. ред. Ю.В.Прохоров, – М.: Сов. энциклопедия, 1988.

7. Молодший В.Н. Основы учения о числе в XVIII и начале XIX века. ― М.: Учпедгиз, 1963.

8. Пискунов Н.С. Дифференциальное и интегральное исчисления. T. 1. – СПб.: Главн. редакция физ–мат. литературы, 1996 и последующие издания.

9. Письменный Д.Т. Конспект лекций по высшей математике. – М.: Айрис-пресс, 2003 (и последующие издания).

10. Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике, вып.2. Пространство, время, движение. – М.: Издательство «Мир», 1965.

[1] Киселёв Андрей Петрович (1852 – 1940) – выдающийся педагог – математик; автор самых популярных отечественных учебников по алгебре и геометрии для средней школы, издававшихся с 1884 по 1972 годы.

[2] Колягин Юрий Михайлович (родился в 1927 году) – заместитель директора Московского педа-гогического НИИ, доктор педагогических наук, профессор.

[3] Эйлер Леонард (Euler Leonhard, 1707–1783) – математик, механик и физик, один из крупнейших учёных XVIII века. Действительный член (академик) Петербургской АН, он жил и работал в Санкт-Петербурге с 1727 по 1741 год, а затем с 1766 года до конца жизни; самый плодовитый математик всех времён и народов.

[4] Нью́тон Исаак (Newton Isaac, 1643 – 1727) – английский физик и математик, создавший теоретические основы механики и астрономии, открывший закон всемирного тяготения, разработавший (наряду с Лейбницем) дифференциальное и интегральное исчисления. Формулу бинома для целых значений показателя степени знали ещё древние китайцы, но названа она в честь Ньютона, поскольку он первый решился на исследование бинома для дробных и отрицательных показателей степени.

[5] Комплексный – (от латинского complexus – связь, сочетание) – совокупный, представляющий собой группу чего-либо.

[6] Фе́йнман (Feynman) Ричард Филлипс (1918 – 1988) – американский физик-теоретик, один из основателей квантовой электродинамики.

[7] Ещё в середине прошлого столетия по тому, как человек произносит прилагательное в сочетаниях «действительные числа» или «вещественные числа», можно было отличить выпускника петербургской математической школы Пафнутия Львовича Чебышёва (читается Чебышёва с ударением на последнем слоге [6; с. 761]) от выпускника московской математической школы Николая Николаевича Лузина.

[8] От латинскогоdisccriminans – ‘различающий, разделяющий’.

[9] Комплексный [от латинского complexus – связь, сочетание] – совокупный, представляющий собой группу каких-либо объектов.

[10] Рене́ Дека́рт (фр. René Descartes, лат. Renatus Cartesius — Картезий, 1596 - 1650) — француз-ский философ и математик, заложивший основы аналитической геометрии.

[11]Обозначения Re и Im – соответственно от латинских reales – действительный, реальный и imaginarius – воображаемый, мнимый.

[12] Любой многочлен с комплексными коэффициентами имеет корень на множестве комплексных чисел. Это означает, что любое уравнение n-ой степени имеет ровно nкорней не обязательно различных; или, что то же самое, любой многочлен n-ой степени с комплексными коэффициентами можно представить произведением n линейных сомножителей.

[13] Муа́вр Абраха́м де (Moivre Abraham de, 1667 – 1754) – английский математик французского происхождения (его родители бежали из Франции по причине религиозных гонений на гугенотов – приверженцев кальвинизма).

[14] Как указывалось во Введении, строгое доказательство этой формулы даётся в последующих двух параграфах с помощью средств, требующих элементарных представлений по теории функций комплексной переменной с использованием сведений из курса степенных рядов и курса дифференциальных уравнений.

[15] Макло́рен Ко́лин (Maclaurin Colin, 1698 – 1746) – шотландский математик, который, будучи с 1719 года секретарём Лондонского королевского общества, имел главной обязанностью отстаивание приоритета Ньютона перед Лейбницем по части открытия дифференциального и интегрального исчислений.

[16] Архимед Сиракузский (Αρχιμηδης , ок. 287–212 до н. э.) – древнегреческий учёный, математик и механик.

[17] В практических расчётах в древнем Египте и древнем Вавилоне дроби применялись уже за две тысячи лет до н. э.

[18] Пифагор Самосский (Πυθαγoρας, ок. 570 – ок. 500 до н.э.) – древнегреческий философ и математик.

[19] Диофант Александрийский (Διοφαντος.) – древнегреческий математик.

[20] Руффи́ни Пао́ло (Ruffini Paolo, 1765–1822) – итальянский математик.

[21] А́́бель Нильс Хе́нрик (Abel Niels Henric, 1802 – 1829) – норвежский математик, впервые исследовавший область сходимости биномиального ряда для комплексных значений переменных

[22] Га́усс Карл Фридрих (Gauss Carl Friedrich, 1777–1855) – выдающийся немецкий математик, внёсший фундаментальный вклад не только в математику, но также в астрономию и геодезию; иностранный член-корреспондент (1802) и иностранный почётный член (1824) Петербургской АН.

[23] Карда́но Джерола́мо (Иеронимус) (Cardano Girolamo, 1501–1576) – итальянский математик, философ и врач.

[24] Бомбе́лли Раффаэ́ле (Bombelli Raffaele, ок. 1530–1572) – итальянский математик и инженер.

[25] Открытие такой зависимости было неожиданностью для самого Эйлера. Великий математик, искренне верящий в сверхъестественные силы, на полях своей рукописи написал: «O, mein Gott! Meine Feder ist kluger als ich! (О, мой Бог! Моё перо умнее меня!)»

[26] Д’Аламбе́р Жан Леро́н (D’Alembert Jean Le Rond; 1717 – 1783) – французский математик и философ, работавший с 1751 года вместе с Д.Дидро над созданием «Энциклопедии наук, искусств и ремёсел».

[27]Лагранж Жозеф Луи (Lagrange Joseph Louis, 1736–1813) – французский математик и механик, иностранный почётный член Петербургской АН (1776).

[28] Берну́лли Якоб (Bernoulli Jacob, 1654–1705) – профессор математики Базельского университета, старший из братьев Бернулли, с которых началась большая семья выдающихся швейцарских учёных

[29]Лапла́с Пьер Симо́н де – французский ученый (Laplace Pierre Simon, 1719 – 1827).

[30] Карно́ Лазар Никола́ Маргери́т (Carno Lasare Nicola Marguerite, 1753–1823) – французский математик, государственный и военный деятель.

[31] Ве́ссель Каспа́р (Wessel Caspar, 1745–1818) – датский математик.

[32] Арга́н Жан Робе́р (Argand Jean Robert, 1768–1822) – швейцарский математик, работавший в Женеве и в Париже.

[33] Коши Огюстен Луи (Cauchy Augustin Louis; 1789 – 1857) – французский математик, основоположник современной теории пределов, иностранный почётный член Петербургской АН (1831).

[34] Вейерштрасс Карл Теодор Вильгельм (Weierstraß Karl Theodor Wilhelm; 1815 – 1897) – немецкий математик, иностранный чл.-корр. (1864) и иностранный почётный член (1895) Петербургской АН.

[35] Га́мильтон Уи́льям Ро́уан (Hamilton William Rowan, 1805–1865) - ирландский математик и астроном, иностранный чл.-корр. Петербургской АН (1837).

[36] Это слово образовано от латинского quaterni – ‘по-четыре’.

[37] Гиперкомплексные числа не являются темой настоящего обзора, поэтому здесь о них лишь упоминается.