
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ФОРМЫ КОМПЛЕКСНЫХ ЧИСЕЛ
Как уже указывалось, комплексное число Z может быть представлено в форме
Z = а + i b (10),
где а = Re Z и b = Im Z.
Такая форма представления комплексных чисел называется алгебраической.
Каждое комплексное число Z = а + ib может быть изображено на плоскости XOY точкой Z(a;b), координатами которой являются соответст-венно действительная и мнимая части этого числа (рис. 1).
Такое изображение комплексного числа называется его геометрической трактовкой (интерпретацией). В этом случае рассматриваемую плоскость называют плоскостью комплексной переменной или просто комплексной плоскостью.
 ImZ
ImZ 



 Z (a;b)
Z (a;b)

|
|

|
| |
 0 ReZ
0 ReZ
Рис. 1
Z = а + i b;
 = а – i b. = а – i b.
|
Действительные числа Z = а + i0 изображаются точками на оси ReZ. Чисто мнимые числа Z = 0 + i b изображаются точками на оси ImZ. При этом ось ОХ называется действительной осью, а ось OY – мнимой.
Два комплексных числа, у которых действительные части равны, а мнимые отличаются только знаком, называются комплексно-сопряжёнными и графически изображаются следующим образом:
| |
|


|
 b
b
|
| |


|
 – b a – i b
– b a – i b
Рис.2
Для точек, соответствующих паре комплексно–сопряжённых чисел, ось ОХ является осью симметри́и.
Полярные координаты ρ и θ точки Z(a;b) называются соответственно модулем (или абсолютной величиной) и аргументом комплексного числа Z.
Они обозначаются:
ρ = ½Z½ (11)
θ = Аrg Z (12)
Здесь угол θ определён с точностью до слагаемого 2pk, где k – целое число. Значение аргумента Z, которое удовлетворяет двойному неравенству
– π  φ
φ  π , (13)
π , (13)
называется главным значением аргумента Z и обозначается arg Z. Тогда получим:
Arg Z = arg Z + 2pk = φ + 2pk (14)
Если |Z|= 0, то в этом единственном случае аргумент считается неопределённым.
Между модулем и аргументом комплексного числа Z = а + ib и
его действительной и мнимой частями очевидны следующие соотношения (рис. 1):
а = | Z | cos θ = ρ cos θ (15)
b = | Z | sin θ = ρ sin θ (16)
Отсюда
ρ = | Z | = 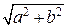 (17)
(17)
cos θ =  =
=  (18)
(18)
sin θ =  =
=  (19)
(19)
Очевидно, что вводя соответствие между точками на плоскости и комплексными числами, мы, тем самым, устанавливаем связь между соответствующими одной и той же точке комплексным числом и радиусом–вектором. Причём действительная и мнимая части комплексного числа будут определять проекции соответствующего радиуса–вектора на оси ОХ и ОУ, т. е. его координаты.
Подставляя (15) и (16) в (10), получим тригонометрическую формулу комплексного числа:
Z = ρ (cos θ + i sin θ) (20)
Пример 1.
Представить на комплексной плоскости число
Z0= - 2 + i3.
Решение дано на рис. 3
 Y
Y
| |

| |


| |
 | |||
 |
Рис. 3
Пример 2.
Представить число Z=– 1 в тригонометрической форме.
Решение:
Для числа Z = – 1 + i0
| Z | = 1; θ = ArgZ = p + 2pк.
Отсюда: –1 = cos (2к + 1) p + i sin (2к + 1) p
При к = 0это выражение принимает наиболее простой вид:
– 1 = cos p + i sin p или Z = cos p
Пример 3.
Представить в тригонометрической форме число
Z= 1 — i  .
.
Решение:
ρ = | Z | = 2; cos θ =  ; sin θ = –
; sin θ = –  .
.
Угол φ находится в четвёртой четверти и поэтому
θ = ArgZ = – 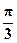 + 2pк; φ = arg Z = –
+ 2pк; φ = arg Z = – 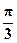 .
.
С учётом cos ( – 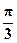 ) = cos
) = cos 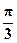 и sin( –
и sin( – 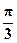 ) = – sin
) = – sin 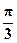 получим (при к = 0)
получим (при к = 0)
1 – i  = 2 (cos
= 2 (cos 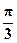 – i sin
– i sin 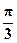 ).
).
Пример 4.
По тригонометрической форме комплексного числа
Z =  (cos
(cos  + i sin
+ i sin  )
)
получить алгебраическую форму.
Решение:
Здесь φ = arg Z=  .
.
Тогда a = | Z | cos φ =  cos
cos  =
=  ∙
∙ 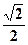 = 1,
= 1,
b = | Z | sin φ =  sin
sin  =
=  ∙
∙ 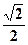 = 1,
= 1,
Z = a + ib = 1 + i
Дата добавления: 2014-11-13; просмотров: 434; Мы поможем в написании вашей работы!; Нарушение авторских прав |