Молекулярно-кинетические свойства коллоидных растворов.

Как показали многочисленные исследования, коллоидные системы по своим молекулярно-кинетическим свойствам принципиально ничем не отличаются от обычных (истинных) растворов, только эти свойства у золей и растворов высокомолекулярных соединений выражены значительно (в сотни и тысячи раз) слабее.

Все их молекулярно-кинетические свойства обусловлены броуновским движением.

Броуновское движение. Частицы дисперсной фазы золя под влиянием ударов молекул растворителя находятся в состоянии непрерывного хаотического движения. Так, если рассматривать какой-либо золь в ультрамикроскоп, можно заметить, что частицы золя все время беспорядочно движутся (рис.6.7).

Впервые это явление было обнаружено английским ботаником Р. Броуном (1827). Он рассматривал суспензию растительной пыльцы в воде в микроскоп и подробно описал беспорядочные колебательные движения (в виде своеобразного, никогда не прекра­щающегося «танца»), совершаемые частицами пыльцы.

Вначале Броун считал, что эти движения присущи только живым существам, но вскоре убедился, что они свойственны любым суспензиям и эмульсиям органических и неорганических ве­ществ при условии, что размер частиц достаточно мал (в пределах от 1 до 5 мкм). Было выдвинуто много различных гипотез для объяснения броуновского движения, но все они каза­лись несостоятельными.

Позднее Гуи (1888) и Экснер (1900) высказали мысль о том, что броуновское движение имеет молекулярно-кинетическую природу, т. е. является следствием теплового движения. Это было впоследствии подтверждено теоретическими расчетами Эйнштейна и Смолуховского, а также экспериментальными работами Перрена и Сведберга.

Опыты показали, что броуновское движение совершенно не зависит от природы вещества; оно изменяется в зависимости от температуры, вязкости среды и размеров частиц. Под действием беспорядочных ударов молекул растворителя частицы дисперсной фазы также совершают беспорядочные движения. Перемещение в пространстве этих частиц совершается в результате усредненного действия всей совокупности ударов за время наблюдения (в 1 с частица испытывает около 1020 ударов). Число ударов, приходящихся с разных сторон, при малых размерах частиц обычно неодинаково и они передвигаются в пространстве по сложной траектории (рис. 6.7). Если размеры и масса частиц дисперсной фазы превышают определенные пределы, вероятность взаимной компенсации ударов оказывается значительно выше. Вот почему частицы размером, например, 4—5 мкм совершают только небольшие колебательные движения около некоторого центра. При более крупных размерах частиц броуновское движение не наблюдается.

Таким образом, наблюдаемое в микроскоп смещение частицы х (рис. 6.7) за определенный промежуток времени является лишь статистическим результатом множества смещений частицы по разным направлениям в пространстве (в их проекции в поле зрения микроскопа). Действительный путь частицы при броуновском движении (как и при молекулярном движении) проследить в ультрамикроскоп невозможно: частица за одну секунду успевает претерпеть десятки и сотни миллионов ударов молекул растворителя и столько же раз ничтожно изменить свое направление, а человеческий глаз способен улавливать не более 10 движений в секунду и притом лишь в крупном масштабе. Это заставило в теорию броуновского движения вместо средней квадратичной скорости для газовых молекул ввести несколько иное понятие — среднее квадратичное смещение, или средний сдвиг ±∆х, как проекцию расстояния между двумя положениями частицы А и В за время t двух смежных наблюдений (рис.6.7). Зависимость среднего смещения частицы ∆х за время t от коэффициента диффузии D выражена Эйнштейном в виде уравнения

6.3

Коэффициент диффузии для сферических частиц, значительно больших по размерам, чем молекулы дисперсионной среды, выражается следующим уравнением:

6.4

Уравнения (6.3) и (6.4) имеют очень большое значение в коллоидной химии, так как позволяют на основании измерений коэффициента диффузии D определить радиус взвешенных коллоидных частиц сферической формы, а также величину молекул высокомолекулярных соединений. Для частиц или макромолекул несферической формы выражение 6πηr в уравнении (6.4) заменяется более сложным.

Подставляя в уравнение (6.3) значение D из уравнения (6.4), для среднего сдвига частицы получим

6.5

Изучение броуновского движения позволило Перрену при содействии математика Ланжевена впервые экспериментально путем непосредственного подсчета в поле зрения ультрамикроскопа определить одну из наиболее важных констант — постоянную Авогадро N₀. Найденное им ее значение N0=6,02·10²³ хорошо согласуется с другими известными данными.

Таким образом, изучение броуновского движения (наряду с ультрамикроскопией) имело большое значение не только для коллоидной химии, но и для всего естествознания в целом как одно из доказательств справедливости диалектико-материалистической концепции миропонимания.

Диффузия и флуктуация. Вследствие молекулярно-кинетического движения частицы дисперсной фазы испытывают случайные смещения, например вверх и вниз. Однако если в каком-либо растворе частицы распределены неравномерно (содержание их у дна сосуда больше, чем в верхнем слое), общее число смещений частиц снизу вверх будет больше, чем сверху вниз. При этом частицы будут передвигаться вверх до тех пор, пока не наступит выравнивание концентраций.

Самопроизвольный процесс выравнивания концентраций ионов, молекул или коллоидно-дисперсных частиц за счет их беспорядочного теплового движения (у коллоидных частиц — броуновского движения) получил название диффузии. Диффузия как самопроизвольный процесс для всех дисперсных систем подчиняется одним и тем же закономерностям, установленным Фиком для газов. Согласно первому закону Фика скорость диффузии прямо пропорциональна площади, через которую происходит диффузия, и градиенту концентрации. Математически этот закон имеет следующее выражение:

6.6

где dm — масса вещества, продиффундировавшего за бесконечно малое время dt через площадь S; dC/dx— падение концентрации на бесконечно малом отрезке диффузионного пути dx, называемое градиентом концентрации; D — коэффициент диффузии, индивидуально характеризующей диффузионную способность данной дисперсной системы. Этот коэффициент выражает количество вещества, диффундирующего в единицу времени (1 с) через единицу пло­щади (1 см²) при градиенте концентрации, равном единице.

С изменением концентрации в процессе диффузии величина градиента концентрации также изменяется. Поэтому необходимо знать скорость изменения концентрации во времени, т. е. производную dC/dt, которая определяется по уравнению, называемому вторым законом Фика:

6.7

Основная трудность в применении обоих законов Фика до недавнего времени заключалась в определении коэффициента диффузии D. Однако трудности определения этого коэффициента для растворов и золей были преодолены после того, как Эйнштейн, изучая броуновское движение, обнаружил связь этого коэффициента со средним сдвигом ∆x . Используя закон Стокса, Эйнштейн нашел зависимость коэффициента диффузии от вязкости среды и радиуса частиц . Диффузионный метод определения размера частиц в настоящее время дает для коллоидных растворов наиболее надежные результаты.

Изучение броуновского движения и диффузии в коллоидных системах помогло глубже вскрыть природу дисперсных систем, а также установить общность молекулярно-кинетических свойств этих систем и систем молекулярной дисперсности. Оно подтвердило реальное существование молекул и явилось убедительным обоснованием правильности материалистического мировоззрения. Дальнейшее более детальное и углубленное изучение броуновского движения привело к созданию так называемой теории флуктуации.

Флуктуация представляет собой самопроизвольное отклонение плотности, концентрации или параметра от среднего равновесного значения в микрообъемах системы. Таким образом, флуктуация представляет собой явление, как бы обратное явлению диффузии, хотя оба они — результат теплово­го движения. Если диффузия как всякий самопроизвольный процесс должна, в соответствии со вторым началом термодинамики, идти необратимо, то флуктуация указывает на то, что второе начало термодинамики имеет статистический характер, т. е. оно неприменимо к отдельным индивидуальным частицам или к малому числу их. В обоих явлениях мы видим одно из доказательств справедливости закона материалистической диалектики—единства противоположностей.

Осмотическое давление. Для коллоидных растворов, как и для истинных, характерно осмотическое давление. Оно, подобно газо­вому давлению, является коллигативным свойством растворов, т. е. зависящим только от числа свободно движущихся коллоидных частиц.

Если учесть, что объем и масса коллоидной частицы значительно больше, чем объем и масса молекулы низкомолекулярных веществ, то при одной и той же весовой концентрации коллоидного и истинного растворов в единице объема золя содержится значительно меньше частиц, чем в единице объема истинного раствора. Вот почему по сравнению с последними коллоидные растворы обладают ничтожно малым осмотическим давлением.

Так, золь золота с массовой концентрацией 10 г/л имеет осмотическое давление, равное 45 Па, а раствор сахарозы той же концентрации и в тех же условиях 7250 Па. Кроме того, какая-то доля измеряемого осмотического давления в коллоидных растворах (главным образом гидрофобных) обусловливается примесью электролитов.

Поскольку коллоидные растворы принципиально не отличаются от истинных растворов, к ним можно применить формулу Вант-Гоффа:

6.8

где П — осмотическое давление золя; n — количество коллоидных частиц (в моль) в V л золя. Под молем коллоидных частиц подразумевается постоянная Авогадро.

Если данный золь содержит ν коллоидных частиц, а 1 моль — N₀ таких же частиц, то n= ν /N₀. С учетом этого уравнение (6.8) примет вид ПV= (ν /N₀)RT, откуда

6.9

Относительно малые концентрации коллоидных растворов обусловливают также ничтожно малые значения всех других величин, зависящих от числа частиц в растворе (частичной концентрации). Так, все коллоидные растворы обладают чрезвычайно малым понижением упругости пара, ничтожными (практически не поддающимися экспериментальному измерению) величинами понижения температур замерзания и повышения температур кипения. Так, Понижение температуры замерзания золя золота концентрации 1 кг/м³ при размере частиц 4 нм равно всего 0,000004°.

Между осмотическим давлением П, числом частиц в единице объема n и средним радиусом коллоидных частиц r можно установить определенную зависимость. Как известно, масса диспергированного вещества в единице объема равна 4/3 πr³dn, где d — плотность раствора. Исходя из этого для двух дисперсных систем с одинаковой дисперсионной средой при одинаковой температуре можно записать: 4/3 πr₁³dn₁ = 4/3 πr₂³dn₂ и r₁³n₁ = r₂³n₂, откуда

6.10

где D — степень дисперсности золя.

Таким образом, осмотическое давление коллоидных растворов обратно пропорционально кубу радиуса частиц и, следовательно, прямо пропорционально кубу степени дисперсности.

Экспериментально осмотическое давление золей измеряют в приборах осмометрах. Для отсчета берут разность давлений в манометре, при которой уровень толуола в капилляре остается постоянным в течение длительного промежутка времени. В этом случае осмотическое давление золя компенсируется внешним давлением. Все измерения осмотического давления необходимо производить при строго постоянной температуре. При измерении давления в манометре и при 25°С осмотическое давление вычисляется по формуле

6.11

где С — концентрация золя или высокомолекулярного соединения; М — относительная молекулярная масса.

Мембранное равновесие Доннана. Более детальное изучение осмотического давления коллоидных растворов показало, что даже применение в качестве внешней жидкости ультрафильтрата этого же золя не дает результатов, которые бы точно соответствовали теоретическим. В некоторых случаях экспериментально определенное осмотическое давление того или иного золя было больше теоретического, оно не зависело в ряде случаев от концентрации коллоида или изменялось не пропорционально концентрации его и т. п. Как показали более углубленные исследования, проведенные в свое время Доннаном, причина подобных отклонений кроется в особом равновесии электролитов, которое устанавливается в присутствии частиц (или ионов), не способных проникать через полупроницаемую мембрану.

Впоследствии само явление неравномерного распределения какого-нибудь электролита по обе стороны полупроницаемой мембраны под влиянием коллоидного электролита получило название мембранного равновесия Доннана.

Рассмотрим основные положения теории мембранного равновесия. Пусть имеется сосуд, разделенный на две части полупроницаемой мембраной, которая способна свободно пропускать ионы электролитов, но задерживает коллоидные частицы. В одной стороне этого сосуда помещен раствор, содержащий электролит Na⁺ и коллоидный анион R^–, задерживаемый мембраной. По другую сторону мембраны в этом же сосуде находится электролит NaCl, оба иона которого могут свободно проходить через мембрану. Состав растворов в сосуде в начале процесса можно представить следующей схемой:

В этой схеме буквами С₁ и С₂ обозначены начальные концентрации соответствующих ионов.

По истечении некоторого промежутка времени ионы Na⁺ и Сl^– начнут свободно проходить из правой половины сосуда в левую. Причем коллоидный анион R^– все время остается в левой половине сосуда. Перемещение ионов закончится установлением динамического равновесия, т. е. количество ионов, переходящих в единицу времени в ту и другую стороны, будет одинаково. Обозначая через х количество ионов Na⁺ и Cl^–, перешедших из правой половины сосуда в левую, состояние равновесия по обе стороны мембраны можно представить следующим образом:

где х не равняется 1/2 С₂, как этого следовало ожидать. Распределение хлорида натрия по обе стороны мембраны не будет равномерным. Ионы, свободно диффундирующие через мембрану, должны распределиться так, чтобы произведение концентраций их в обоих отсеках сосуда было одинаковым, т. е

6.12

Решая это уравнение относительно х, получим

6.13

Доля электролита NaCl, которая перешла из правой части сосуда в левый, будет равна:

6.14

Анализ уравнений (6.13) и (6.14) показывает, что если концентрация электролита велика по сравнению с концентрацией коллоида, т. е. С₂>>С₁ то x/С₂≈1/2. В этом случае электролит NaCl распределяется поровну по обе стороны мембраны. Этот вывод имеет чрезвычайно важное практическое значение, так как экспериментально определенное осмотическое давление золя наиболее близко к расчетному. Таким образом, более точные значения осмотического давления золя могут получиться при избытке электролита в ультрафильтрате.

Если концентрация электролита очень мала по сравнению с концентрацией коллоида С₂<<С₁ то х/С₂≈0, т. е. электролит практически не переходит из правой половины сосуда в левую.

Доннановское равновесие имеет очень большое значение для понимания и теоретического обоснования целого ряда явлений: осмотического давления лиофобных коллоидов и растворов высокомолекулярных соединений, отрицательной адсорбции ионов, явлений набухания, а также различных физиологических процессов.

Седиментационное равновесие. Частицы вещества, диспергированного в жидкой или газообразной среде, постоянно находятся под влиянием двух противоположно направленных сил — силы тяжести, под действием которой частицы данного вещества оседают, и сил диффузии, под влиянием которых частицы стремятся переместиться из области больших в область меньших концентраций, т. е. к равномерному распределению в объеме.

В зависимости от преобладания тех или иных сил в системе наблюдается осаждение частиц дисперсной фазы (под влиянием сил тяжести) или (в случае преобладания сил диффузии) выравнивание концентрации во всем объеме системы. Процесс оседания частиц под действием силы тяжести носит название седиментации (от лат. sedimentum — оседание). Скорость оседания частиц зависит не только от их размера, но и от разности плотностей частиц d—d₀, а также от вязкости этой среды η и математически выражается следующим уравнением:

6.15

где υ — скорость оседания частиц; r — радиус частиц; d и d₀ — плотности диспергированного вещества и растворителя; η — вязкость среды, g — ускорение силы тяжести.

Из уравнения (6.15) видно, что с большей скоростью оседают более крупные частицы. Так, частицы серебра оседают в воде на 1 см при r = 1 · 10^{-4 м за 0,05 с; при r =1·10-6 м — за 500 с, а при r =1·10-8 см — за 58 суток. Диффузия в случае более мелких частиц дисперсной фазы протекает с большей скоростью и замедляется с увеличением их размера. Если степень дисперсности вещества мала (радиус частиц больше 2 нм), то частицы не совершают броуновского движения, следовательно, их способность к диффузии равна нулю. В данном случае сила тяжести значительно преобладает над силами диффузии.}

Если в системе силы тяжести полностью уравновешены силами диффузии, наступает так называемое седиментационное равновесие, которое характеризуется равенством скоростей седиментации и диффузии. При этом через единицу поверхности сечения в единицу времени проходит вниз столько же оседающих частиц, сколько их проходит вверх с диффузионным потоком. Седиментационное равновесие наблюдается не только в коллоидных растворах, но и в молекулярно-дисперсных системах. Это равновесие характеризуется постепенным уменьшением концентрации частиц в направлении от нижних слоев к верхним. Распределение частиц в зависимости от высоты столба жидкости подчиняется гипсометрическому (или барометрическому) закону Лапласа в применении к золям: при увеличении высоты столба золя в арифметической прогрессии концентрация частиц убывает в геометрической прогрессии. Математически этот закон выражается в виде уравнения

6.16

где С₁ — концентрация дисперсной системы на исходном уровне; С₂ — концентрация этой системы на высоте h; M — относительнаямолекулярная масса веще­ства; g — ускорение силы тяжести.

На определении скорости оседания частиц дисперсной фазы основаны все методы седиментационного анализа. Определив экспериментально скорость оседания частиц, можно рассчитать их размер, т. е. степень дисперсности. Размер радиуса дисперсной частицы можно определить из уравнения (6.17)):

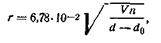
6.17

Поскольку оседание частиц коллоидной степени дисперсности под действием силы тяжести происходит медленно, для его ускорения применяют ультрацентрифуги, которые способны развивать центробежную силу, примерно в

1 000 000 раз превосходящую силу земного тяготения. Именно при помощи ультрацентрифуги были определены размеры частиц в некоторых коллоидах, а также молекулярные массы большого числа полимерных соединений.

Таблица 6.4

В табл. 6.4 приведены данные по определению частичной (моле­кулярной) массы некоторых белковых веществ, определенных с помощью метода ультрацентрифугирования.

Суспензии и эмульсии с размером частиц в интервале 1— 200 мкм изучаются простыми методами седиментации в так называемых седиментометрах. Результаты седиментационного анализа обычно изображают графически в виде кривой распределения, на которой по оси абсцисс наносятся значения радиуса частиц, а по оси ординат — процентное содержание частиц данной фракции, отнесенное к определенному интервалу радиусов. По данным седиментационного анализа можно, например, определять удельную поверхность порошкообразных веществ, а также наиболее вероятный радиус диспергированных частиц.