Тензор напряжения.

Для уяснения дальнейшего необходимо подробней рассмотреть вектор .

В движущейся среде мысленно выделим частицу в форме жидкого тетраэдра. Пусть - внешняя нормаль к четвертой (на­клонной) грани тетраэдра , а площадь этой грани dS (см. рис. 2.4).

Площади других граней - соответственно , , , 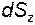т.к. их можно рассматривать как проекции грани ABC на координатные оси. Следовательно, , где обозначает направляющий косинус. Аналогично, , . Обозначим объем тетраэдра dV, тогда действующая на него массовая сила , а массовая сила инерции , где вектор ускорения жидкого тетраэд­ра. Поверхностная сила, действующая на наклонную грань - . Для трех других граней можем записать:

Знаки минус, т.к. векторы , и направлены в стороны, противоположные координатным осям.

Запишем уравнение движения тетраэдра, которое в соответ­ствии с общими законами механики должно иметь вид:

Масса ускорение = (результирующая массовых сил) +

+ (результирующая поверхностных сил).

Имеем:

Слагаемые 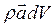и есть величины третьего порядка малости, а остальные - второго, поэтому ими можно пренебречь, что дает

(2.9)

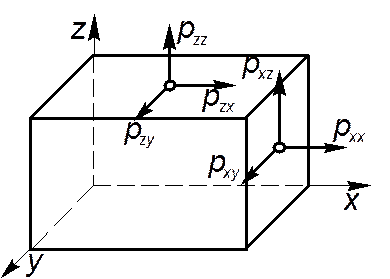
Из этого равенства следует, что напряжение 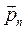при произвольной ориентации нормали может быть определено, если известны напряжения в той же точке для площадок, внешние нормали которых параллельны осям Ox, Oy и Oz.

Проекции векторов , и 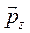на координатные оси x, y, z обозначаются:

Первый подстрочный индекс указывает ось, перпендикулярную ориентации площадки, второй ­ ось, на которую спроектировано напряжение.

Для уяснения ориентации рассмотрим параллелепипед, выделенный в движущейся жидкости и показанный на рис. 2.5.

Из рисунка, в частности, видно, что напряжения с одинаковыми индексами являются нормальными, а с разными - касательными. В проекциях на декартовы оси координат выражение (2.9) может быть записано как

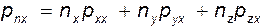
(2.10)

Совокупность этих девяти составляющих компонентов напряжения образует тензор напряжения. В матричной форме он записывается в следующем виде:

В тензорном анализе доказывается, что тензор напряжений является симметричным. Это означает, что величины, расположен­ные симметрично главной диагонали, равны ( ; ; ). Следовательно, для определения тензора напряжений достаточно знать не девять, а шесть скалярных величин.

Следует учесть одно обстоятельство. Векторы напряжений 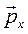, , в соотношении (2.9), носящем имя Коши, и приложенные к координатным площадкам, не имеют объективного физического смысла, т.к. зависят от выбора системы координат. Поэтому такие величины причисляются к так называемым «квазивекторам», хотя к ним и можно применять все операции, применимые к физическим векторам.

К понятию тензора можно подойти и другим путем, который, возможно, покажется более простым. Поэтому целесообразно хотя бы кратко остановиться на нем. Для наглядности тензор можно представить как какой-то оператор, с помощью которого можно преобразовывать векторы в векторы. Упрощая и сводя математический аппарат к механическому, оператор можно представить как какую-то «машину», которая по определенным правилам перерабатывает вводимые в нее векторы. Зная принцип работы этой «машины», можем знать и вектор, который появляется на выходе. Можно записать

где - входной вектор;

- выходной вектор;

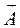- оператор, который и называют тензором.

Существенное ограничение заключается в том, что оператор должен быть линейным. Определить тензор - это значит задать правила, по которым работает оператор. Для интересующихся таким подходом можно рекомендовать книгу Астарита Дж., Марручи Дж. Основы гидромеханики неньютоновских жидкостей. - М.: Мир, 1978.-307с.

И в заключение еще несколько замечаний. Выше уже отмечалось, что одно из фундаментальных свойств жидкости ­ ее вязкость ­ не проявляется, если она находится в состоянии равновесия, т.е. в этом случае касательные компоненты тензора равны нулю и действуют лишь нормальные , , , ориентированные по внешним нормалям (см. рис. 2.5). При этом ясно, что они являются растягивающими напряжениями. Как показывает опыт, в отличие от твердого тела, которое может воспринимать как растягивающие (положительные нормальные напряжения), так и сжимающие (отрицательные нормальные напряжения) напряжения без разрыва сплошности, жидкое тело способно воспринимать лишь сжимающие усилия. Можно показать, что при отсутствии касательных напряжений , из чего следует, что нормальные напряжения в данной точке не зависят от ориентации площадки. Величины, численно равные нормальным напряжениям, но взятые с противоположным знаком, в гидромеханике называют давлениями, либо более полно ­ гидростатическими давлениями. Гидростатическое давление обозначают буквой p, т.е.

Таким образом, гидростатическое давление, являясь скалярной величиной (как компонента тензора) не зависит от ориентации площадки, на которую оно действует.

Теоретическое изучение движения жидкости связано с так называемой моделью идеальной жидкости. В этой модели жидкость рассматривается как абсолютно несжимаемая среда, неспособная сопротивляться разрывающим усилиям и обладающая абсолютной подвижностью, т.е. лишенная вязкости. Последнее исключает возникновение в ней касательных напряжений.