Операции второго порядка.

Операции , , 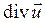, переводящие скаляр в вектор, вектор в скаляр и вектор в вектор порождают пять операций второго порядка:

- превращение скалярной величины в векторную

;

- превращение векторной величины в скалярную

;

;

- превращение одной векторной величины в другую

;

.

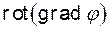В теории поля показывается, что два из этих пяти соотношений тождественно равны нулю: и . Операция носит название оператора Лапласа для скалярного поля и имеет вид

(1.9)

Интегральные соотношения теории поля.

Поток векторного поля.

Пусть dS (рис. 1.1) - элемент поверхности, а 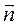- единичный вектор, направленный по внешней нормали. Потоком векторного поля (например, ) называют поверхностный интеграл вида

(1.10)

Если рассматривается векторное поле ротора ( 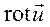), то поток этого поля представляется как

(1.11)